题目内容
10. 如图,AB是⊙O的直径,C是⊙O上一点,∠ACD=∠B,AD⊥CD.
如图,AB是⊙O的直径,C是⊙O上一点,∠ACD=∠B,AD⊥CD.(1)求证:CD是⊙O的切线;
(2)若AD=1,OA=2,求CD的值.
分析 (1)连接OB,由圆周角定理得出∠ACB=90°,由等腰三角形的性质得出∠B=∠BCO,证出∠OCD=∠OCA+∠BCO=∠ACB=90°,即可得出结论;
(2)证明△ACB∽△ADC,得出AC2=AD•AB,根据勾股定理即可得出结果.
解答  (1)证明:连接OC,如图所示:
(1)证明:连接OC,如图所示:
∵AB是⊙O直径,
∴∠ACB=90°,
∵OB=OC,
∴∠B=∠BCO,
又∵∠ACD=∠B,
∴∠OCD=∠OCA+∠ACD=∠OCA+∠BCO=∠ACB=90°,
即OC⊥CD,
∴CD是⊙O的切线;
(2)解:∵AD⊥CD,
∴∠ADC=∠ACB=90°,
又∵∠ACD=∠B,
∴△ACB∽△ADC,
∴AC2=AD•AB=1×4=4,
∴AC=2,
∴CD=$\sqrt{A{C}^{2}-A{D}^{2}}$=$\sqrt{3}$.
点评 本题考查了切线的判定、等腰三角形的性质、相似三角形的判定与性质;熟练掌握切线的判定,证明三角形相似是解决问题(2)的关键.

练习册系列答案
相关题目
18.下列关于$\sqrt{10}$的说法中,错误的是( )
| A. | $\sqrt{10}$是无理数 | B. | $3<\sqrt{10}<4$ | ||
| C. | 10的平方根是$\sqrt{10}$ | D. | $\sqrt{10}$是10的算术平方根 |
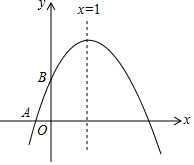 如图,已知二次函数y=ax2+bx+c(a≠0)的图象与x轴交于点A(-1,0),顶点坐标为(1,n),与y轴的交点在(0,2)和(0,3)之间(不包括端点).有下列结论:①当x>3时,y<0;②n=c-a;③3a+b>0;④-1<a<-$\frac{2}{3}$.其中正确的结论有( )
如图,已知二次函数y=ax2+bx+c(a≠0)的图象与x轴交于点A(-1,0),顶点坐标为(1,n),与y轴的交点在(0,2)和(0,3)之间(不包括端点).有下列结论:①当x>3时,y<0;②n=c-a;③3a+b>0;④-1<a<-$\frac{2}{3}$.其中正确的结论有( )
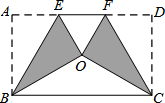 将矩形纸片ABCD按如图方式折叠,BE、CF为折痕,折叠后点A和点D都落在点O处,若△EOF是等边三角形,则$\frac{AB}{AD}$的值为$\frac{\sqrt{3}}{3}$.
将矩形纸片ABCD按如图方式折叠,BE、CF为折痕,折叠后点A和点D都落在点O处,若△EOF是等边三角形,则$\frac{AB}{AD}$的值为$\frac{\sqrt{3}}{3}$.