题目内容
2.已知今年小明爸爸的年龄是37岁,小明的年龄是12岁,那么再过13年,小明爸爸的年龄是小明年龄的2倍.分析 本题中存在的等量关系是:x年后,小明爸爸的年龄=小明年龄的2倍.可以设再过x年,这个等量关系中的两个量:小明爸爸的年龄和小明年龄都可以表示出来,就可列方程求解.
解答 解:设再过x年,小明爸爸的年龄是小明年龄的2倍,依题意有
37+x=2(12+x),
解得x=13.
答:再过13年,小明爸爸的年龄是小明年龄的2倍.
故答案为:13.
点评 此题主要考查了一元一次方程的应用,列方程的关键是能用代数式正确表示出等量关系中的各个部分.

练习册系列答案
相关题目
12.某公司为了扩大经营,决定购进6台机器用于生产某种活塞,现有甲、乙两种机器共选择,其中每种机器的价格和每台机器日生产活塞的数量如下表所示:
经过预算,本次购买机器所耗资金不能超过34万元.
(1)按该公司要求可以有几种购买方案?
(2)若该公司购进的6台机器的日生产能力不能低于380个,那么为了节约资金应选择哪种购买方案?
| 甲 | 乙 | |
| 价格/(万元/台) | 7 | 5 |
| 每台日产量/个 | 100 | 60 |
(1)按该公司要求可以有几种购买方案?
(2)若该公司购进的6台机器的日生产能力不能低于380个,那么为了节约资金应选择哪种购买方案?
13.下列运算正确的是( )
| A. | (-a-b)2=a2-2ab+b2 | B. | 2a+3b=5ab | C. | 3a2÷a2=3 | D. | (-x2)•(-x)3=-x5 |
10.下列各曲线中,不能表示y是x的函数的是( )
| A. |  | B. |  | C. |  | D. |  |
17.如果一个角的补角等于它余角的4倍,那么这个角的度数是( )
| A. | 30° | B. | 45° | C. | 60° | D. | 90° |
12.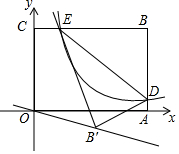 如图,平面直角坐标系xOy中,矩形OABC的边OA、OC分别落在x、y轴上,点B坐标为(6,4),反比例函数y=$\frac{6}{x}$的图象与AB边交于点D,与BC边交于点E,连结DE,将△BDE沿DE翻折至△B'DE处,点B'恰好落在正比例函数y=kx图象上,则k的值是( )
如图,平面直角坐标系xOy中,矩形OABC的边OA、OC分别落在x、y轴上,点B坐标为(6,4),反比例函数y=$\frac{6}{x}$的图象与AB边交于点D,与BC边交于点E,连结DE,将△BDE沿DE翻折至△B'DE处,点B'恰好落在正比例函数y=kx图象上,则k的值是( )
 如图,平面直角坐标系xOy中,矩形OABC的边OA、OC分别落在x、y轴上,点B坐标为(6,4),反比例函数y=$\frac{6}{x}$的图象与AB边交于点D,与BC边交于点E,连结DE,将△BDE沿DE翻折至△B'DE处,点B'恰好落在正比例函数y=kx图象上,则k的值是( )
如图,平面直角坐标系xOy中,矩形OABC的边OA、OC分别落在x、y轴上,点B坐标为(6,4),反比例函数y=$\frac{6}{x}$的图象与AB边交于点D,与BC边交于点E,连结DE,将△BDE沿DE翻折至△B'DE处,点B'恰好落在正比例函数y=kx图象上,则k的值是( )| A. | $-\frac{2}{5}$ | B. | $-\frac{1}{21}$ | C. | $-\frac{1}{5}$ | D. | $-\frac{1}{24}$ |