题目内容
11.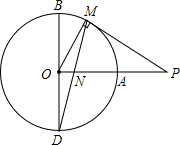 如图,BD是⊙O的直径,OA⊥OB,点M是劣弧AB上一动点(不与点A、B重合),过点M作⊙O的切线MP交OA的延长线于点P,MD与OA交于点N.
如图,BD是⊙O的直径,OA⊥OB,点M是劣弧AB上一动点(不与点A、B重合),过点M作⊙O的切线MP交OA的延长线于点P,MD与OA交于点N.(1)求证:PM=PN;
(2)当点M运动到何处时,△PMN是等边三角形?请说明理由.
分析 (1)利用切线的性质得到OM⊥PM和BD⊥OA得出互余的关系,即可;
(2)利用互余得到∠BDM=30°即可.
解答 (1)证明:∵BD⊥OA,
∴∠AOD=90°,
∴∠ODM+∠OND=90°,
∵OD=OM,
∴∠ODM=∠OMD,
∴∠OMD+∠OND=90°
∵PM切⊙O于M,
∴∠OMD+∠PMN=90°,
∴∠OND=∠PMN,
∵∠OND=∠MNP,
∴∠PMN=∠MNP,
∴PM=PN;
(2)当点M运动到满足,$\widehat{BM}$=2$\widehat{AM}$(∠BOM=60°)时,△PMN是等边三角形
由(1)有,∠PMN=∠MNP,
∵△PMN是等边三角形,
∴∠MNP=60°,
∴∠OND=60°,
∴∠ODM=30°,
∴$\widehat{BM}$=2$\widehat{AM}$(∠BOM=60°).
点评 此题是圆的切线,主要考查了圆的切线的性质,同角的与角相等,角的等量代换是解本题的关键.

练习册系列答案
相关题目
2.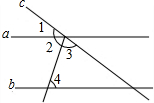 如图,直线a,b被直线c所截,a∥b,若∠2=∠3,∠4=63°,则∠1等于( )
如图,直线a,b被直线c所截,a∥b,若∠2=∠3,∠4=63°,则∠1等于( )
 如图,直线a,b被直线c所截,a∥b,若∠2=∠3,∠4=63°,则∠1等于( )
如图,直线a,b被直线c所截,a∥b,若∠2=∠3,∠4=63°,则∠1等于( )| A. | 54° | B. | 58° | C. | 63° | D. | 68° |
 如图,已知抛物线y=ax2+bx+c与x轴的两个交点A、B坐标分别为(-1,0),(-3,0),抛物线与y轴交点C为(0,3).
如图,已知抛物线y=ax2+bx+c与x轴的两个交点A、B坐标分别为(-1,0),(-3,0),抛物线与y轴交点C为(0,3).
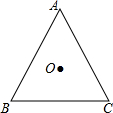 如图,△ABC是边长为1的等边三角形,点O是△ABC的中心.
如图,△ABC是边长为1的等边三角形,点O是△ABC的中心.