题目内容
20.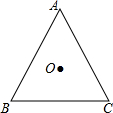 如图,△ABC是边长为1的等边三角形,点O是△ABC的中心.
如图,△ABC是边长为1的等边三角形,点O是△ABC的中心.(1)作出△ABC以O为旋转中心,沿逆时针方向旋转180°得到的△A1B1C1;
(2)求△ABC与△A1B1C1重叠部分的面积.
分析 (1)根据中心旋转的定义,作出图形即可.
(2)重叠部分是正六边形,是由边长为$\frac{1}{3}$的6个等边三角形组成的,利用边长为a等边三角形的面积=$\frac{\sqrt{3}}{4}$a2进行计算即可.
解答 解:(1)△ABC以O为旋转中心,沿逆时针方向旋转180°得到的△A1B1C1图象如图所示,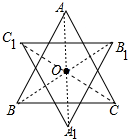
(2)△ABC与△A1B1C1重叠部分是边长为$\frac{1}{3}$的正六边形,所以重叠部分面积=6×$\frac{\sqrt{3}}{4}$×($\frac{1}{3}$)2=$\frac{\sqrt{3}}{6}$.
点评 本题考查旋转作图、正六边形、等边三角形的有关知识,解题的关键是正确连接中心旋转的定义,记住等边三角形的面积公式,正六边形与等边三角形之间的关系,属于中考常考题型.

练习册系列答案
 鸿图图书寒假作业假期作业吉林大学出版社系列答案
鸿图图书寒假作业假期作业吉林大学出版社系列答案
相关题目
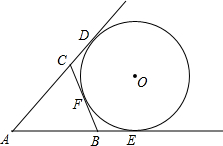
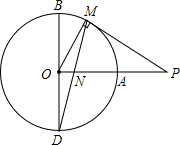 如图,BD是⊙O的直径,OA⊥OB,点M是劣弧AB上一动点(不与点A、B重合),过点M作⊙O的切线MP交OA的延长线于点P,MD与OA交于点N.
如图,BD是⊙O的直径,OA⊥OB,点M是劣弧AB上一动点(不与点A、B重合),过点M作⊙O的切线MP交OA的延长线于点P,MD与OA交于点N.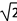 x+2=0的根的情况为( )
x+2=0的根的情况为( )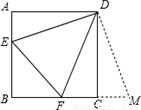
 如图,△ABC的周长等于16,圆O与BC相切于点F,AB、AC的延长线与圆分别相切于点E、D,求AE的长.
如图,△ABC的周长等于16,圆O与BC相切于点F,AB、AC的延长线与圆分别相切于点E、D,求AE的长. 如图,一条笔直的公路经过两个城镇A和B,为了改善居住条件,当地要建设一个新城镇C,已知新城镇C在城镇A的北偏东30°方向距城镇A 8km处,且位于城镇B的正北方向,已知AB=4$\sqrt{2}$km,求新城镇C到公路的距离.(结果保留到0.1km,参考数据:$\sqrt{3}$≈1.73,$\sqrt{2}$≈1.41,$\sqrt{6}$≈2.45)
如图,一条笔直的公路经过两个城镇A和B,为了改善居住条件,当地要建设一个新城镇C,已知新城镇C在城镇A的北偏东30°方向距城镇A 8km处,且位于城镇B的正北方向,已知AB=4$\sqrt{2}$km,求新城镇C到公路的距离.(结果保留到0.1km,参考数据:$\sqrt{3}$≈1.73,$\sqrt{2}$≈1.41,$\sqrt{6}$≈2.45)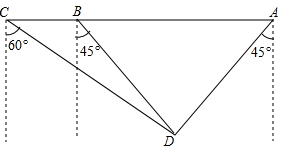 如图,某海监船向正西方向航行,在A处望见一艘正在作业渔船D在南偏西45°方向上,海监船航行到B处时望见渔船D在南偏东45°方向上,又航行了半小时到达C处,望见渔船D在南偏东60°方向上,若海监船的速度为40海里/时,求A,B之间的距离.(结果保留根号)
如图,某海监船向正西方向航行,在A处望见一艘正在作业渔船D在南偏西45°方向上,海监船航行到B处时望见渔船D在南偏东45°方向上,又航行了半小时到达C处,望见渔船D在南偏东60°方向上,若海监船的速度为40海里/时,求A,B之间的距离.(结果保留根号)