题目内容
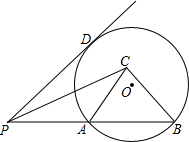如图，PD切⊙O于D，PC=PD，B为⊙O上一点，PB交⊙O于A，连结AC、BC．求证：AC•PB=PC•BC．考点：切线的性质,相似三角形的判定与性质
专题：证明题
分析：由切割线定理可得PD2=PA•PB，即有PC2=PA•PB，可证明△PAC∽△PCB，利用相似三角形的对应边成比例可证得结论．
解答：证明：
∵PD切⊙O于D，PB交⊙O于A，
∴PD2=PA•PB，
∵PC=PD，
∴PC2=PA•PB，即
=
，
又∠APC=∠CPB，
∴△PAC∽△PCB，
∴
=
，
即AC•PB=PC•BC．
∵PD切⊙O于D，PB交⊙O于A，
∴PD2=PA•PB，
∵PC=PD，
∴PC2=PA•PB，即
| PC |
| PB |
| PA |
| PC |
又∠APC=∠CPB，
∴△PAC∽△PCB，
∴
| AC |
| BC |
| PC |
| PB |
即AC•PB=PC•BC．
点评：本题主要考查切线的性质和相似三角形的判定，利用切割线定理得到三角形相似的条件是解题的关键，注意相似三角形对应边成比例的应用．
练习册系列答案
Happy holiday欢乐假期暑假作业广东人民出版社系列答案
快乐暑假暑假能力自测中西书局系列答案
相关题目
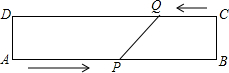如图，在矩形ABCD中，AB=20 cm，动点P从点A开始沿AB边以4 cm/s的速度运动，动点Q从点C开始沿CD边以1 cm/s的速度运动，点P和点Q同时出发，当其中一点到达终点时，另一点也随之停止运动，运动点的运动时间为t s，则当t为何值时，四边形APQD时矩形？
正方形ABCD与正方形DEFG的边长分别是8和5，E在AD的延长线上，G在CD的延长线上，求△ACF的面积．
如图，Rt△ABC中，∠ACB=90°，∠A=35°，D为AB中点，CE⊥AB，则∠DCE=
如图，已知AB∥CD，直线EF分别交AB，CD于点E，F，EG平分∠AEF，若∠1=38°，求∠2的度数．
如图，在⊙O中，半径OA=8cm，cos∠A=