题目内容
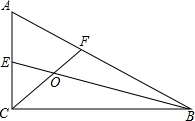 如图,∠ACB=90°,∠ABC=30°,BE、CF分别平分∠ABC、∠ACB,交AC、AB于点E、F,BE,CF交于点O,求证:OE=OF.
如图,∠ACB=90°,∠ABC=30°,BE、CF分别平分∠ABC、∠ACB,交AC、AB于点E、F,BE,CF交于点O,求证:OE=OF.考点:全等三角形的判定与性质
专题:证明题
分析:在BC上找到一点G,使得CG=CE,易证∠OCE=∠OCG即可证明△OCE≌△OCG,可得∠COE=∠COG,OE=OG,即可求得∠BOG=∠BOF,即可证明△BOG≌△BOF,可得OF=OG,即可解题.
解答:证明:在BC上找到一点G,使得CG=CE,
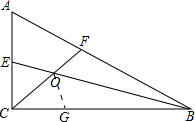
∵CF平分∠ACB,
∴∠OCE=∠OCG=45°,
在△OCE和△OCG中,
,
∴△OCE≌△OCG(SAS),
∴∠COE=∠COG,OE=OG,
∵BE平分∠ABC,
∴∠CBE=∠ABE=15°,
∴∠BEC=75°,
∴∠COE=∠COG=60°,
∴∠BOG=∠BOF=60°,
在△BOG和△BOF中,
,
∴△BOG≌△BOF(ASA),
∴OF=OG,
∴OE=OF.

∵CF平分∠ACB,
∴∠OCE=∠OCG=45°,
在△OCE和△OCG中,
|
∴△OCE≌△OCG(SAS),
∴∠COE=∠COG,OE=OG,
∵BE平分∠ABC,
∴∠CBE=∠ABE=15°,
∴∠BEC=75°,
∴∠COE=∠COG=60°,
∴∠BOG=∠BOF=60°,
在△BOG和△BOF中,
|
∴△BOG≌△BOF(ASA),
∴OF=OG,
∴OE=OF.
点评:本题考查了全等三角形的判定,考查了全等三角形对应边相等的性质,考查了三角形内角和为180°的性质,本题中求证△OCE≌△OCG和△BOG≌△BOF是解题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
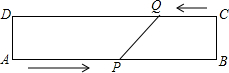 如图,在矩形ABCD中,AB=20 cm,动点P从点A开始沿AB边以4 cm/s的速度运动,动点Q从点C开始沿CD边以1 cm/s的速度运动,点P和点Q同时出发,当其中一点到达终点时,另一点也随之停止运动,运动点的运动时间为t s,则当t为何值时,四边形APQD时矩形?
如图,在矩形ABCD中,AB=20 cm,动点P从点A开始沿AB边以4 cm/s的速度运动,动点Q从点C开始沿CD边以1 cm/s的速度运动,点P和点Q同时出发,当其中一点到达终点时,另一点也随之停止运动,运动点的运动时间为t s,则当t为何值时,四边形APQD时矩形? 如图,菱形ABCD中,CF⊥AD垂足为E,交BD的延长线于F,求证:AO2=BO•OF.
如图,菱形ABCD中,CF⊥AD垂足为E,交BD的延长线于F,求证:AO2=BO•OF. 正方形ABCD与正方形DEFG的边长分别是8和5,E在AD的延长线上,G在CD的延长线上,求△ACF的面积.
正方形ABCD与正方形DEFG的边长分别是8和5,E在AD的延长线上,G在CD的延长线上,求△ACF的面积. 如图,Rt△ABC中,∠ACB=90°,∠A=35°,D为AB中点,CE⊥AB,则∠DCE=
如图,Rt△ABC中,∠ACB=90°,∠A=35°,D为AB中点,CE⊥AB,则∠DCE= 如图,已知A、B、C、D四点在⊙O上,AB、CD交于点E,AD=BC,求证:AB=CD.
如图,已知A、B、C、D四点在⊙O上,AB、CD交于点E,AD=BC,求证:AB=CD.