题目内容
7.一个不透明的袋子中装有红、白两种颜色的小球,这些球除颜色外都相同,其中红球有1个,若从中随机摸出一个球,这个球是白球的概率为$\frac{2}{3}$.(1)求袋子中白球的个数;(请通过列式或列方程解答)
(2)随机摸出一个球后,放回并搅匀,再随机摸出一个球,求两次都摸到相同颜色的小球的概率.(请结合树状图或列表解答)
分析 (1)首先设袋子中白球有x个,利用概率公式求即可得方程:$\frac{x}{x+1}$=$\frac{2}{3}$,解此方程即可求得答案;
(2)首先根据题意画出树状图,然后由树状图求得所有等可能的结果与两次都摸到相同颜色的小球的情况,再利用概率公式即可求得答案.
解答 解:(1)设袋子中白球有x个,
根据题意得:$\frac{x}{x+1}$=$\frac{2}{3}$,
解得:x=2,
经检验,x=2是原分式方程的解,
∴袋子中白球有2个;
(2)画树状图得:
∵共有9种等可能的结果,两次都摸到相同颜色的小球的有5种情况,
∴两次都摸到相同颜色的小球的概率为:$\frac{5}{9}$.
点评 此题考查了列表法或树状图法求概率.注意掌握方程思想的应用.注意概率=所求情况数与总情况数之比.

练习册系列答案
相关题目
2.若关于x的方程x2+(m+1)x+$\frac{1}{2}$=0的一个实数根的倒数恰是它本身,则m的值是( )
| A. | -$\frac{5}{2}$ | B. | $\frac{1}{2}$ | C. | -$\frac{5}{2}$或$\frac{1}{2}$ | D. | 1 |
12.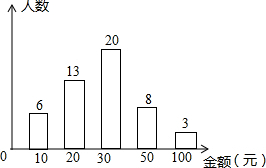 随着智能手机的普及,抢微信红包成为了春节期间人们最喜欢的活动之一.某中学九年级五班班长对全班50名学生在春节期间所抢的红包金额进行统计,并绘制成了统计图.根据如图提供的信息,红包金额的众数和中位数分别是( )
随着智能手机的普及,抢微信红包成为了春节期间人们最喜欢的活动之一.某中学九年级五班班长对全班50名学生在春节期间所抢的红包金额进行统计,并绘制成了统计图.根据如图提供的信息,红包金额的众数和中位数分别是( )
 随着智能手机的普及,抢微信红包成为了春节期间人们最喜欢的活动之一.某中学九年级五班班长对全班50名学生在春节期间所抢的红包金额进行统计,并绘制成了统计图.根据如图提供的信息,红包金额的众数和中位数分别是( )
随着智能手机的普及,抢微信红包成为了春节期间人们最喜欢的活动之一.某中学九年级五班班长对全班50名学生在春节期间所抢的红包金额进行统计,并绘制成了统计图.根据如图提供的信息,红包金额的众数和中位数分别是( )| A. | 20、20 | B. | 30、20 | C. | 30、30 | D. | 20、30 |
12.某书店准备购进甲、乙两种图书共100本,购书款不高于2224元,预这100本图书全部售完的利润不低于1100元,两种图书的进价、售价如表所示:
请回答下列问题:
(1)书店有多少种进书方案?
(2)在这批图书全部售出的条件下,(1)中的哪种方案利润最大?最大利润是多少?(请你用所学的函数知识来解决)
| 甲种图书 | 乙种图书 | |
| 进价(元/本) | 16 | 28 |
| 售价(元/本) | 26 | 40 |
(1)书店有多少种进书方案?
(2)在这批图书全部售出的条件下,(1)中的哪种方案利润最大?最大利润是多少?(请你用所学的函数知识来解决)
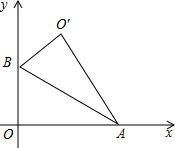 如图,Rt△AOB中,∠AOB=90°,OA在x轴上,OB在y轴上,点A,B的坐标分别为($\sqrt{3}$,0),(0,1),把Rt△AOB沿着AB对折得到Rt△AO′B,则点O′的坐标为($\frac{\sqrt{3}}{2}$,$\frac{3}{2}$)..
如图,Rt△AOB中,∠AOB=90°,OA在x轴上,OB在y轴上,点A,B的坐标分别为($\sqrt{3}$,0),(0,1),把Rt△AOB沿着AB对折得到Rt△AO′B,则点O′的坐标为($\frac{\sqrt{3}}{2}$,$\frac{3}{2}$).. 如图,埃航MS804客机失事后,国家主席亲自发电进行慰问,埃及政府出动了多艘舰船和飞机进行搜救,其中一艘潜艇在海面下500米的A点处测得俯角为45°的前下方海底有黑匣子信号发出,继续沿原方向直线航行2000米后到达B点,在B处测得俯角为60°的前下方海底有黑匣子信号发出,求海底黑匣子C点距离海面的深度(结果保留根号).
如图,埃航MS804客机失事后,国家主席亲自发电进行慰问,埃及政府出动了多艘舰船和飞机进行搜救,其中一艘潜艇在海面下500米的A点处测得俯角为45°的前下方海底有黑匣子信号发出,继续沿原方向直线航行2000米后到达B点,在B处测得俯角为60°的前下方海底有黑匣子信号发出,求海底黑匣子C点距离海面的深度(结果保留根号).


