题目内容
已知sin6°=a,sin36°=b,则sin26°=( )
A. a2 B. 2a C. b2 D. b
 A
【解析】∵sin6°=a,
∴=a2.
故选:A.
A
【解析】∵sin6°=a,
∴=a2.
故选:A.
 寒假大串联黄山书社系列答案
寒假大串联黄山书社系列答案△ABC中,三个内角的度数均为整数,且∠A<∠B<∠C,4∠C=7∠A,求∠A的度数.
 44°
【解析】试题分析:先用∠A表示出∠C,再根据三角形的内角和等于180°列式整理用
∠A表示出∠B,再根据不等式求出∠A的取值范围,最后根据∠A是整数解答.
试题解析:
∵4∠C=7∠A,
∵∠A<∠B<∠C,
由①得,
由②得,
∵∠A,∠C是整数,
∴∠A是4的整数倍,
44°
【解析】试题分析:先用∠A表示出∠C,再根据三角形的内角和等于180°列式整理用
∠A表示出∠B,再根据不等式求出∠A的取值范围,最后根据∠A是整数解答.
试题解析:
∵4∠C=7∠A,
∵∠A<∠B<∠C,
由①得,
由②得,
∵∠A,∠C是整数,
∴∠A是4的整数倍, 下列分式是最简分式的是( )
A. 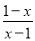 B.
B. 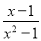
C. 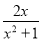 D.
D. 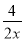
 C
【解析】根据最简分式的特点,分子分母没有公因式,因此A可化为,不是最简分式;B可化为,不是最简分式;C是最简分式;D可化简为,不是最简分式.
故选:C.
C
【解析】根据最简分式的特点,分子分母没有公因式,因此A可化为,不是最简分式;B可化为,不是最简分式;C是最简分式;D可化简为,不是最简分式.
故选:C. 如图,在Rt△ABC中,∠C=90°,AB=2BC,则sinB的值为 .
 【解析】试题分析:因为在Rt△ABC中,∠C = 90°,AB = 2BC,所以.
【解析】试题分析:因为在Rt△ABC中,∠C = 90°,AB = 2BC,所以. 如图,学校大门出口处有一自动感应栏杆,点A是栏杆转动的支点,当车辆经过时,栏杆AE会自动升起,某天早上,栏杆发生故障,在某个位置突然卡住,这时测得栏杆升起的角度∠BAE=127°,已知AB⊥BC,支架AB高1.2米,大门BC打开的宽度为2米,以下哪辆车可以通过?( )(栏杆宽度,汽车反光交镜忽略不计)(参考数据:sin37°≈0.60,cos37°≈0.80,tan37°≈0.75,车辆尺寸:长×宽×高)
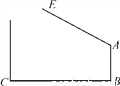
A. 宝马Z4(4200 mm×1800 mm×1360 mm) B. 奇瑞QQ(4000 mm×1600 mm×1520 mm)
C. 大众朗逸(4600 mm×1700 mm×1400 mm) D. 奥迪A4(4700 mm×1800 mm×1400 mm)
 C
【解析】试题解析:如图,过点A作BC的平行线AG,过点N作NQ⊥BC于Q,交AG于点R,
则∠BAG=90°,
∵∠BAE=127°,∠BAG=90°,
∴∠EAH=∠EAB-∠BAG=37°.
在△NAR中,∠ARN=90°,∠EAG=37°,
当车宽为1.8m,则GR=1.8m,故AR=2-1.8=0.2(m),
∴NR=ARtan37°=0.2×...
C
【解析】试题解析:如图,过点A作BC的平行线AG,过点N作NQ⊥BC于Q,交AG于点R,
则∠BAG=90°,
∵∠BAE=127°,∠BAG=90°,
∴∠EAH=∠EAB-∠BAG=37°.
在△NAR中,∠ARN=90°,∠EAG=37°,
当车宽为1.8m,则GR=1.8m,故AR=2-1.8=0.2(m),
∴NR=ARtan37°=0.2×... Rt△ABC中,∠C=90°,AB=10,BC=8,求cosB的值.
 【解析】分析: 直接利用锐角三角函数关系得出cosB.
本题解析:
∵∠C=90°,AB=10,BC=8,
∴cosB=
故答案为:
【解析】分析: 直接利用锐角三角函数关系得出cosB.
本题解析:
∵∠C=90°,AB=10,BC=8,
∴cosB=
故答案为: 如图,将∠AOB放在边长为1的小正方形组成的网格中,则tan∠AOB= .
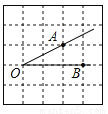
 .
【解析】试题分析:过点A作AD⊥OB垂足为D,如图,在直角△ABD中,AD=1,OD=2,则tan∠AOB==.故答案为: .
.
【解析】试题分析:过点A作AD⊥OB垂足为D,如图,在直角△ABD中,AD=1,OD=2,则tan∠AOB==.故答案为: . 某移动通信公司开设了两种通信业务,“全球通”:使用时首先缴50元月租费,然后每通话1分钟,付话费0.4元;“动感地带”:不缴月租费,每通话1分钟,付话费0.6元(本题的通话均指市内通话).若一个月通话x分钟,两种方式的费用分别为y1元和y2元.
(1)写出y1,y2与x之间的关系式;
(2)一个月内通话多少分钟,两种方式费用相同?
(3)某人估计一个月内通话300分钟,应选择哪种方式更合算些?
 【解析】
(1)y1=50+0.4x,y2=0.6x (2)当每个月通话250分钟时,两种方式费用相同 (3)使用“全球通”合算
【解析】试题分析:(1)理解每种通信业务的付费方式,依据每分钟通话费用×通话时长便可确定每种方式的费用,进而写出y1、y2的关系式;
对于(2),令y1=y2,解方程即可;
对于(3),令x=300,分别求出y1、y2的值,再做比较即可.
【解...
【解析】
(1)y1=50+0.4x,y2=0.6x (2)当每个月通话250分钟时,两种方式费用相同 (3)使用“全球通”合算
【解析】试题分析:(1)理解每种通信业务的付费方式,依据每分钟通话费用×通话时长便可确定每种方式的费用,进而写出y1、y2的关系式;
对于(2),令y1=y2,解方程即可;
对于(3),令x=300,分别求出y1、y2的值,再做比较即可.
【解... 在△ABC中,AB=AC,且BC=8cm,BD是腰AC的中线,△ABC的周长分为两部分,已知它们的差为2cm,则等腰三角形的腰长为__________.
 10cm或6cm
【解析】如图∵BD是腰AC的中线,
∴AD=CD,
①当△ABD的周长与△BCD的周长差为2时,即AB+AD+BD-(BD+BC+CD)=2,
∴AB-BC=2,
∵BC=8cm,
∴AB=10cm.
②当△BCD的周长与△ABD的周长差为2时,即BD+BC+CD -(AB+AD+BD)=2,
∴BC - AB =2,
∵BC...
10cm或6cm
【解析】如图∵BD是腰AC的中线,
∴AD=CD,
①当△ABD的周长与△BCD的周长差为2时,即AB+AD+BD-(BD+BC+CD)=2,
∴AB-BC=2,
∵BC=8cm,
∴AB=10cm.
②当△BCD的周长与△ABD的周长差为2时,即BD+BC+CD -(AB+AD+BD)=2,
∴BC - AB =2,
∵BC... 
