题目内容
18.先化简,再求值:($\frac{1}{x-2}$+$\frac{1}{x+2}$)•(x2-4),其中x=$\sqrt{5}$.分析 先计算括号内分式的加法,再计算乘法即可化简原式,将x的值代入求解可得.
解答 解:原式=[$\frac{x+2}{(x+2)(x-2)}$+$\frac{x-2}{(x+2)(x-2)}$]•(x+2)(x-2)
=$\frac{2x}{(x+2)(x-2)}$•(x+2)(x-2)
=2x,
当x=$\sqrt{5}$时,
原式=2$\sqrt{5}$.
点评 本题主要考查分式的化简求值,熟练掌握分式的混合运算顺序和法则是解题的关键.

练习册系列答案
相关题目
8.当a=$\sqrt{2}$时,计算分式$\frac{a+3}{a}$•$\frac{6}{{a}^{2}+6a+9}$+$\frac{2a-6}{{a}^{2}-9}$的值是$\sqrt{2}$.
10.如图是某几何体的三视图,这个几何体是( )


| A. | 圆锥 | B. | 长方体 | C. | 圆柱 | D. | 三棱柱 |
7.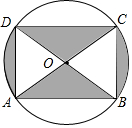 如图是某商品的标志图案,AC与BD是⊙O的两条直径,首尾顺次连接点A,B,C,D,得到四边形ABCD.若AC=10cm,∠BAC=36°,则图中阴影部分的面积为( )
如图是某商品的标志图案,AC与BD是⊙O的两条直径,首尾顺次连接点A,B,C,D,得到四边形ABCD.若AC=10cm,∠BAC=36°,则图中阴影部分的面积为( )
 如图是某商品的标志图案,AC与BD是⊙O的两条直径,首尾顺次连接点A,B,C,D,得到四边形ABCD.若AC=10cm,∠BAC=36°,则图中阴影部分的面积为( )
如图是某商品的标志图案,AC与BD是⊙O的两条直径,首尾顺次连接点A,B,C,D,得到四边形ABCD.若AC=10cm,∠BAC=36°,则图中阴影部分的面积为( )| A. | 5πcm2 | B. | 10πcm2 | C. | 15πcm2 | D. | 20πcm2 |
8.气温由-2℃上升3℃后是( )℃.
| A. | 1 | B. | 3 | C. | 5 | D. | -5 |
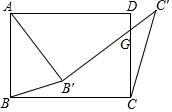 如图,在矩形ABCD中,将∠ABC绕点A按逆时针方向旋转一定角度后,BC的对应边B'C'交CD边于点G.连接BB'、CC'.若AD=7,CG=4,AB'=B'G,则$\frac{CC'}{{{B}{B}'}}$=$\frac{\sqrt{74}}{5}$(结果保留根号).
如图,在矩形ABCD中,将∠ABC绕点A按逆时针方向旋转一定角度后,BC的对应边B'C'交CD边于点G.连接BB'、CC'.若AD=7,CG=4,AB'=B'G,则$\frac{CC'}{{{B}{B}'}}$=$\frac{\sqrt{74}}{5}$(结果保留根号).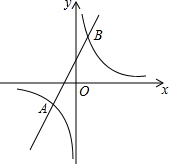 如图,直线y=2x+4与反比例函数y=$\frac{k}{x}$的图象相交于A(-3,a)和B两点
如图,直线y=2x+4与反比例函数y=$\frac{k}{x}$的图象相交于A(-3,a)和B两点 已知:如图,圆锥的底面直径是10cm,高为12cm,则它的侧面展开图的面积是65πcm2.
已知:如图,圆锥的底面直径是10cm,高为12cm,则它的侧面展开图的面积是65πcm2.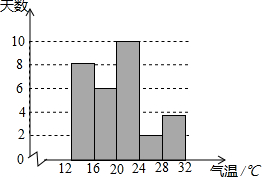 为了解某地某个季度的气温情况,用适当的抽样方法从该地这个季度中抽取30天,对每天的最高气温x(单位:℃)进行调查,并将所得的数据按照12≤x<16,16≤x<20,20≤x<24,24≤x<28,28≤x<32分成五组,得到如图频数分布直方图.
为了解某地某个季度的气温情况,用适当的抽样方法从该地这个季度中抽取30天,对每天的最高气温x(单位:℃)进行调查,并将所得的数据按照12≤x<16,16≤x<20,20≤x<24,24≤x<28,28≤x<32分成五组,得到如图频数分布直方图.