题目内容
7.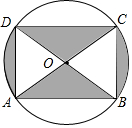 如图是某商品的标志图案,AC与BD是⊙O的两条直径,首尾顺次连接点A,B,C,D,得到四边形ABCD.若AC=10cm,∠BAC=36°,则图中阴影部分的面积为( )
如图是某商品的标志图案,AC与BD是⊙O的两条直径,首尾顺次连接点A,B,C,D,得到四边形ABCD.若AC=10cm,∠BAC=36°,则图中阴影部分的面积为( )| A. | 5πcm2 | B. | 10πcm2 | C. | 15πcm2 | D. | 20πcm2 |
分析 根据已知条件得到四边形ABCD是矩形,求得图中阴影部分的面积=S扇形AOD+S扇形BOC=2S扇形AOD,根据等腰三角形的性质得到∠BAC=∠ABO=36°,由圆周角定理得到∠AOD=72°,于是得到结论.
解答 解:∵AC与BD是⊙O的两条直径,
∴∠ABC=∠ADC=∠DAB=∠BCD=90°,
∴四边形ABCD是矩形,
∴△ABO与△CDO的面积的和=△AOD与△BOC的面积的和,
∴图中阴影部分的面积=S扇形AOD+S扇形BOC=2S扇形AOD,
∵OA=OB,
∴∠BAC=∠ABO=36°,
∴∠AOD=72°,
∴图中阴影部分的面积=2×$\frac{72•π×{5}^{2}}{360}$=10π,
故选B.
点评 本题考查了扇形的面积,矩形的判定和性质,圆周角定理,熟练掌握扇形的面积公式是解题的关键.

练习册系列答案
相关题目
2. 甲、乙两组各有12名学生,组长绘制了本组5月份家庭用水量的统计图表,如图,
甲、乙两组各有12名学生,组长绘制了本组5月份家庭用水量的统计图表,如图,
甲组12户家庭用水量统计表
比较5月份两组家庭用水量的中位数,下列说法正确的是( )
 甲、乙两组各有12名学生,组长绘制了本组5月份家庭用水量的统计图表,如图,
甲、乙两组各有12名学生,组长绘制了本组5月份家庭用水量的统计图表,如图,甲组12户家庭用水量统计表
| 用水量(吨) | 4 | 5 | 6 | 9 |
| 户数 | 4 | 5 | 2 | 1 |
| A. | 甲组比乙组大 | B. | 甲、乙两组相同 | C. | 乙组比甲组大 | D. | 无法判断 |
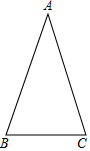 已知等腰△ABC的顶角∠A=36°(如图).
已知等腰△ABC的顶角∠A=36°(如图).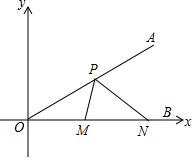 如图,∠AOB的边OB与x轴正半轴重合,点P是OA上的一动点,点N(3,0)是OB上的一定点,点M是ON的中点,∠AOB=30°,要使PM+PN最小,则点P的坐标为($\frac{3}{2}$,$\frac{\sqrt{3}}{2}$).
如图,∠AOB的边OB与x轴正半轴重合,点P是OA上的一动点,点N(3,0)是OB上的一定点,点M是ON的中点,∠AOB=30°,要使PM+PN最小,则点P的坐标为($\frac{3}{2}$,$\frac{\sqrt{3}}{2}$).