题目内容
3.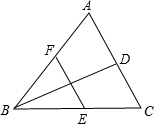 如图,点D、E、F分别是AC、BC、AB中点,且 BD是△ABC的角平分线.求证:BE=AF.
如图,点D、E、F分别是AC、BC、AB中点,且 BD是△ABC的角平分线.求证:BE=AF.
分析 连接DE,根据三角形中位线定理和平行四边形的判定定理证明四边形ADEF是平行四边形,得到AF=DE,证明BE=DE,等量代换即可.
解答 证明:连接DE,
∵点D、E、F分别是AC、BC、AB中点.
∴DE∥AB,EF∥AC,
∴四边形ADEF是平行四边形,
∴AF=DE,
∵BD是△ABC的角平分线,
∴∠ABD=∠DBE,
∴∠DBE=∠BDE,
∴BE=DE,
∴BE=AF.
点评 本题考查的是三角形中位线定理,掌握三角形的中位线平行于第三边,并且等于第三边的一半是解题的关键.

练习册系列答案
相关题目
14.直角三角形中,如果有两条边长分别为3,4,且第三条边长为整数,那么第三条边长应该是( )
| A. | 5 | B. | 4 | C. | 3 | D. | 2 |
8.下列运算正确的是( )
| A. | -2x(3x2y-2xy)=-6x2y-4x2y | B. | 2x2y(-x2+2y+1)=-4x3y4 | ||
| C. | (3ab2-2ab)abc=3a2b2-2a2b2 | D. | (ab)2(2ab2c)=2a3b4c |
13.教师节来临,某校举办了以感恩为主题的贺卡制作比赛,赛后整理参赛学生的成绩,并制作成如表:
请根据如图表提供的信息解答下列问题:
(1)表中a、b、c所表示的数分别是:a=95,b=90,c=0.3;
(2)参赛学生比赛成绩的中位数落在哪个分数段?求出参赛学生成绩的平均得分;
(3)如果比赛成绩80分以上(含80分)可获得奖励,那么获奖率是多少?
| 分数段/分 | 组中值 | 频数(人数) | 频率 |
| 60≤x<70 | 65 | 30 | 0.15 |
| 70≤x<80 | 75 | b | 0.45 |
| 80≤x<90 | 85 | 60 | c |
| 90≤x<100 | a | 20 | 0.1 |
(1)表中a、b、c所表示的数分别是:a=95,b=90,c=0.3;
(2)参赛学生比赛成绩的中位数落在哪个分数段?求出参赛学生成绩的平均得分;
(3)如果比赛成绩80分以上(含80分)可获得奖励,那么获奖率是多少?
 如图,△ABC中,AB=AC,E、F分别是BC、AC的中点,以AC为斜边作Rt△ADC.
如图,△ABC中,AB=AC,E、F分别是BC、AC的中点,以AC为斜边作Rt△ADC. 如图是“赵爽弦图”,△ABH、△BCG、△CDF和△DAE是四个全等的直角三角形,四边形ABCD和EFGH都是正方形,如果AB=10,EF=2,那么AH为a,BH为b,则ab=48.
如图是“赵爽弦图”,△ABH、△BCG、△CDF和△DAE是四个全等的直角三角形,四边形ABCD和EFGH都是正方形,如果AB=10,EF=2,那么AH为a,BH为b,则ab=48.