题目内容
 如图,在⊙O中,弦AB与直径CD垂直,垂足为E,则下列结论中错误的是( )
如图,在⊙O中,弦AB与直径CD垂直,垂足为E,则下列结论中错误的是( )| A、AE=BE |
| B、CE=DE |
| C、弧AC=弧BC |
| D、弧AD=弧BD |
考点:垂径定理
专题:
分析:回顾一下垂径定理的内容,根据定理得出AE=BE,弧AD=弧BD,弧AC=弧BC,即可得出选项.
解答:解:∵CD⊥AB,CD为直径,
∴AE=BE,弧AD=弧BD,弧AC=弧BC,
CE>DE,
故选B.
∴AE=BE,弧AD=弧BD,弧AC=弧BC,
CE>DE,
故选B.
点评:本题考查了垂径定理的应用,解此题的关键是能正确理解定理的内容,注意:垂直于弦的直径平分这条弦,并且平分弦所对的每一条弧.

练习册系列答案
 金钥匙试卷系列答案
金钥匙试卷系列答案
相关题目
在矩形ABCD中,AB=4,AD=2,O是CD的中点,以点O为圆心画图,使得A,B,C,D四点中有两点在圆内,有两点在圆外,则⊙O的半径r的取值范围是( )
A、2
| ||
B、2<r<2
| ||
| C、2<r<3 | ||
| D、3<r<4 |
在Rt△ABC,∠C=90°,sinB=
,则sinA的值是( )
| 3 |
| 5 |
A、
| ||
B、
| ||
C、
| ||
D、
|
 已知:抛物线C1:y=-
已知:抛物线C1:y=-
| ||
| 3 |
| 3 |
| 5 |
| 3 |
| 3 |
| A、向左平移3个单位 | ||||
| B、向右平移6个单位 | ||||
C、向右平移
| ||||
| D、向左平移6个单位 |
 如图,点M在射线OA上,点N在射线OB上,芳芳在直线MN上求作一点P,使它到OA、OB的距离相等,则点P是( )
如图,点M在射线OA上,点N在射线OB上,芳芳在直线MN上求作一点P,使它到OA、OB的距离相等,则点P是( )| A、线段MN的中点 |
| B、OA与OB的中垂线的交点 |
| C、OA与MN的中垂线的交点 |
| D、MN与∠AOB的平分线的交点 |
下列各数为负数的是( )
| A、0 | B、-2014 |
| C、-(-1) | D、|-1| |
 如图,AD,BE,CF依次是△ABC的高、中线和角平分线,下列表达式中错误的是( )
如图,AD,BE,CF依次是△ABC的高、中线和角平分线,下列表达式中错误的是( )| A、AE=CE |
| B、∠ADC=90° |
| C、∠CAD=∠CBE |
| D、∠ACB=2∠ACF |
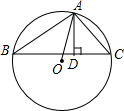 如图,已知△ABC内接于⊙O,AD为BC边上的高.
如图,已知△ABC内接于⊙O,AD为BC边上的高. 有一块边长为2米的正方形苗圃ABCD,园林师傅想把它设计成如图所示的图案.分别以正方形ABCD的四个顶点为圆心,2米长为半径作弧,在中间阴影部分上种上薰衣草,则薰衣草的占地面积是
有一块边长为2米的正方形苗圃ABCD,园林师傅想把它设计成如图所示的图案.分别以正方形ABCD的四个顶点为圆心,2米长为半径作弧,在中间阴影部分上种上薰衣草,则薰衣草的占地面积是