题目内容
14. 如图,矩形ABCD的面积S,对角线交于点O;以AB、AO为邻边做平行四边形AOC1B,对角线交于点O1;以AB、AO1为邻边作平行四边形AO1C2B;…;以此类推,则平行四边形AOnCn+1B的面积为$\frac{S}{{2}^{n+1}}$.
如图,矩形ABCD的面积S,对角线交于点O;以AB、AO为邻边做平行四边形AOC1B,对角线交于点O1;以AB、AO1为邻边作平行四边形AO1C2B;…;以此类推,则平行四边形AOnCn+1B的面积为$\frac{S}{{2}^{n+1}}$.
分析 由矩形的性质和面积公式得出:平行四边形AOC1B的面积=$\frac{1}{2}$S,平行四边形AO1C2B的面积=$\frac{S}{{2}^{2}}$,…,根据规律,即可得出结果.
解答 解:根据题意得:平行四边形AOC1B的面积=$\frac{1}{2}$矩形ABCD的面积=$\frac{1}{2}$S,
平行四边形AO1C2B的面积=$\frac{1}{2}$平行四边形AOC1B的面积=$\frac{1}{4}$S=$\frac{S}{{2}^{2}}$,…,
平行四边形AOn-1CnB的面积=$\frac{S}{{2}^{n}}$,
∴平行四边形AOnCn+1B的面积=$\frac{S}{{2}^{n+1}}$;
故答案为:$\frac{S}{{2}^{n+1}}$.
点评 本题考查了矩形的性质、平行四边形面积的计算;熟练掌握矩形的性质,根据题意得出规律是解决问题的关键.

练习册系列答案
相关题目
5. 如图,点E在正方形ABCD内,满足∠AEB=90°,AE=6,BE=8,则阴影部分的面积是( )
如图,点E在正方形ABCD内,满足∠AEB=90°,AE=6,BE=8,则阴影部分的面积是( )
 如图,点E在正方形ABCD内,满足∠AEB=90°,AE=6,BE=8,则阴影部分的面积是( )
如图,点E在正方形ABCD内,满足∠AEB=90°,AE=6,BE=8,则阴影部分的面积是( )| A. | 76 | B. | 70 | C. | 48 | D. | 24 |
9.2015年3月31日安岳县一彩民喜中双色球(一种彩票)一等奖,奖金近900万元,你可知道,双色球一注号码中一等奖的可能性大约只有0.0000000564,所以买彩票一定要理性.请用科学记数法表示0.0000000564为( )
| A. | -5.64×108 | B. | -5.64×107 | C. | 5.64×10-8 | D. | 5.64×10-7 |
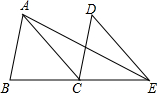 如图,将△ABC沿射线BC方向移动,使点B移动到点C,得到△DCE,连接AE,若△ABC的面积为2,则△ACE的面积为( )
如图,将△ABC沿射线BC方向移动,使点B移动到点C,得到△DCE,连接AE,若△ABC的面积为2,则△ACE的面积为( ) 如图,F是正方形ABCD的边CD上的一个动点,BF的垂直平分线交对角线AC于点E,连结BE,BF,则∠EBF的度数是多少?
如图,F是正方形ABCD的边CD上的一个动点,BF的垂直平分线交对角线AC于点E,连结BE,BF,则∠EBF的度数是多少? 已知:如图,在△ABC中,AC∥DE,DC∥FE,CD平分∠BCA.求证:EF平分∠BED.
已知:如图,在△ABC中,AC∥DE,DC∥FE,CD平分∠BCA.求证:EF平分∠BED.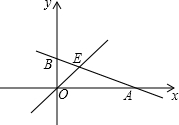 如图,已知函数y=-$\frac{1}{3}x+b$的图象与x轴、y轴分别交于点A、B,与函数y=x的图象交于点E,点E的横坐标为3.
如图,已知函数y=-$\frac{1}{3}x+b$的图象与x轴、y轴分别交于点A、B,与函数y=x的图象交于点E,点E的横坐标为3.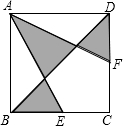 已知正方形ABCD,E为BC的中点,DF=$\frac{1}{2}$CF,求阴影部分占正方形面积的几分之几?
已知正方形ABCD,E为BC的中点,DF=$\frac{1}{2}$CF,求阴影部分占正方形面积的几分之几?