题目内容
2. 如图,F是正方形ABCD的边CD上的一个动点,BF的垂直平分线交对角线AC于点E,连结BE,BF,则∠EBF的度数是多少?
如图,F是正方形ABCD的边CD上的一个动点,BF的垂直平分线交对角线AC于点E,连结BE,BF,则∠EBF的度数是多少?
分析 过E作HI∥BC,分别交AB、CD于点H、I,证明Rt△BHE≌Rt△EIF,可得∠IEF+∠HEB=90°,再根据BE=EF即可解题.
解答 解:如图所示,过E作HI∥BC,分别交AB、CD于点H、I,则∠BHE=∠EIF=90°,
∵E是BF的垂直平分线EM上的点,
∴EF=EB,
∵E是∠BCD角平分线上一点,
∴E到BC和CD的距离相等,即BH=EI,
Rt△BHE和Rt△EIF中,
$\left\{\begin{array}{l}{EF=BE}\\{BH=EI}\end{array}\right.$,
∴Rt△BHE≌Rt△EIF(HL),
∴∠HBE=∠IEF,
∵∠HBE+∠HEB=90°,
∴∠IEF+∠HEB=90°,
∴∠BEF=90°,
∵BE=EF,
∴∠EBF=∠EFB=45°.
点评 本题考查了正方形角平分线和对角线重合的性质,考查了直角三角形全等的判定,全等三角形对应角相等的性质.

练习册系列答案
 全能测控期末小状元系列答案
全能测控期末小状元系列答案
相关题目
12.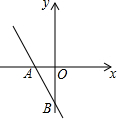 如图所示,一次函数y=(m-2)x-4的图象分别与x轴、y轴的负半轴相交于A,B,则m的取值范围是( )
如图所示,一次函数y=(m-2)x-4的图象分别与x轴、y轴的负半轴相交于A,B,则m的取值范围是( )
 如图所示,一次函数y=(m-2)x-4的图象分别与x轴、y轴的负半轴相交于A,B,则m的取值范围是( )
如图所示,一次函数y=(m-2)x-4的图象分别与x轴、y轴的负半轴相交于A,B,则m的取值范围是( )| A. | m>2 | B. | m<2 | C. | m>0 | D. | m<0 |
17.下列语句:①每一个外角都等于60°的多边形是六边形;②“反证法”就是举反例说明一个命题是假命题;③“等腰三角形两底角相等”的逆命题是真命题;④分式有意义的条件是分子为零且分母不为零.其中正确的个数为( )
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
7. 如图,在平行四边形ABCD中,CE⊥AB,E为垂足.如果∠A=118°,则∠BCE=( )
如图,在平行四边形ABCD中,CE⊥AB,E为垂足.如果∠A=118°,则∠BCE=( )
 如图,在平行四边形ABCD中,CE⊥AB,E为垂足.如果∠A=118°,则∠BCE=( )
如图,在平行四边形ABCD中,CE⊥AB,E为垂足.如果∠A=118°,则∠BCE=( )| A. | 28° | B. | 38° | C. | 62° | D. | 72° |
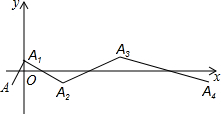 如图,一个动点A在平面直角坐标系中作折线运动,第一次从点(-1,-1)到A1(0,1),第二次运动到A2(3,-1),第三次运动到A3(8,1),第四次运动到A4(15,-1)…,按这样的运动规律,经过第11次运动后,动点A11的坐标是(120,1).
如图,一个动点A在平面直角坐标系中作折线运动,第一次从点(-1,-1)到A1(0,1),第二次运动到A2(3,-1),第三次运动到A3(8,1),第四次运动到A4(15,-1)…,按这样的运动规律,经过第11次运动后,动点A11的坐标是(120,1). 如图,矩形ABCD的面积S,对角线交于点O;以AB、AO为邻边做平行四边形AOC1B,对角线交于点O1;以AB、AO1为邻边作平行四边形AO1C2B;…;以此类推,则平行四边形AOnCn+1B的面积为$\frac{S}{{2}^{n+1}}$.
如图,矩形ABCD的面积S,对角线交于点O;以AB、AO为邻边做平行四边形AOC1B,对角线交于点O1;以AB、AO1为邻边作平行四边形AO1C2B;…;以此类推,则平行四边形AOnCn+1B的面积为$\frac{S}{{2}^{n+1}}$.