题目内容
3.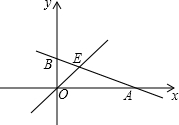 如图,已知函数y=-$\frac{1}{3}x+b$的图象与x轴、y轴分别交于点A、B,与函数y=x的图象交于点E,点E的横坐标为3.
如图,已知函数y=-$\frac{1}{3}x+b$的图象与x轴、y轴分别交于点A、B,与函数y=x的图象交于点E,点E的横坐标为3.(1)求点A的坐标;
(2)在x轴上有一点F(a,0),过点F作x轴的垂线,分别交函数y=-$\frac{1}{3}x+b$和y=x的图象于点C、D,若以点B、O、C、D为顶点的四边形为平行四边形,求a的值.
分析 (1)把x=3代入y=x,求出y的值,确定出E坐标,把E坐标代入函数解析式求出b的值,确定出函数解析式,即可求出A的坐标;
(2)根据题意得到C与D横坐标都为a,分别代入两直线解析式表示出C与D的纵坐标,进而表示出CD的长,由B、O、C、D为顶点的四边形为平行四边形,得到CD=OB,即可求出a的值.
解答  解:(1)把x=3代入y=x,得:y=3,即E(3,3),
解:(1)把x=3代入y=x,得:y=3,即E(3,3),
把E坐标代入y=-$\frac{1}{3}$x+b中,得:b=4,即函数解析式为y=-$\frac{1}{3}$x+4,
令y=0,得到x=12,
则A(12,0);
(2)直线AB解析式为y=-$\frac{1}{3}$x+4,
由题意可知,C、D的横坐标为a,
∴C(a,-$\frac{1}{3}$a+4),D(a,a),
∴CD=a-(-$\frac{1}{3}$a+4)=$\frac{4}{3}$a-4,
若以点B、O、C、D为顶点的四边形为平行四边形,
∴CD=OB=4,即$\frac{4}{3}$a-4=4,
解得:a=6.
点评 此题属于一次函数综合题,涉及的知识有:一次函数与坐标轴的交点,坐标与图形性质,平行四边形的性质,以及待定系数法求一次函数解析式,熟练掌握待定系数法是解本题的关键.

练习册系列答案
相关题目
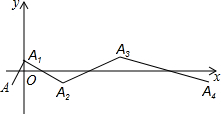 如图,一个动点A在平面直角坐标系中作折线运动,第一次从点(-1,-1)到A1(0,1),第二次运动到A2(3,-1),第三次运动到A3(8,1),第四次运动到A4(15,-1)…,按这样的运动规律,经过第11次运动后,动点A11的坐标是(120,1).
如图,一个动点A在平面直角坐标系中作折线运动,第一次从点(-1,-1)到A1(0,1),第二次运动到A2(3,-1),第三次运动到A3(8,1),第四次运动到A4(15,-1)…,按这样的运动规律,经过第11次运动后,动点A11的坐标是(120,1). 如图,矩形ABCD的面积S,对角线交于点O;以AB、AO为邻边做平行四边形AOC1B,对角线交于点O1;以AB、AO1为邻边作平行四边形AO1C2B;…;以此类推,则平行四边形AOnCn+1B的面积为$\frac{S}{{2}^{n+1}}$.
如图,矩形ABCD的面积S,对角线交于点O;以AB、AO为邻边做平行四边形AOC1B,对角线交于点O1;以AB、AO1为邻边作平行四边形AO1C2B;…;以此类推,则平行四边形AOnCn+1B的面积为$\frac{S}{{2}^{n+1}}$.
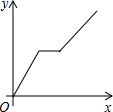
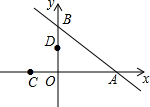 如图,在平面直角坐标系xOy中,直线y=-$\frac{3}{4}$x+3与x轴交于点A,与y轴交于点B,将△AOB沿过点A的直线折叠,使点B落在x轴负半轴上,记得点C,折痕与y轴交于点D,则点D的坐标为(0,$\frac{4}{3}$).
如图,在平面直角坐标系xOy中,直线y=-$\frac{3}{4}$x+3与x轴交于点A,与y轴交于点B,将△AOB沿过点A的直线折叠,使点B落在x轴负半轴上,记得点C,折痕与y轴交于点D,则点D的坐标为(0,$\frac{4}{3}$).