题目内容
6．
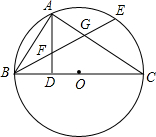如图，BC是⊙O的直径，点A在⊙O上，AD⊥BC，垂足为D，$\widehat{AE}$=$\widehat{AB}$，BE分别交AD、AC于点F、G，判断△FAG的形状，并说明理由．
分析 由BC是⊙O的直径，得到∠BAC=90°，于是得到∠ABE+∠AGB=90°，由于AD⊥BC，得到∠C+∠DAC=90°，等量代换得到∠FAG=∠AGF，于是得到结论．
解答 解：∵BC是⊙O的直径，
∴∠BAC=90°，
∴∠ABE+∠AGB=90°，
∵AD⊥BC，
∴∠C+∠DAC=90°，
∵$\widehat{AE}$=$\widehat{AB}$，
∴∠ABE=∠C，
∴∠FAG=∠AGF，
∴△FAG是等腰三角形．
点评 本题考查了圆周角定理，直角三角形的性质，等腰三角形的判定，熟练掌握圆周角定理是解题的关键．
练习册系列答案
相关题目
在同一直角坐标系中，画出下列函数的图象：
17．一元二次方程2x2+5x+2=0的根的情况是（ ）
| A． | 有两个相等的实数根 | B． | 有两个不相等的实数根 | ||
| C． | 无实数根 | D． | 不能确定 |
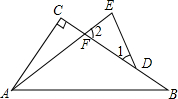如图，在△ABC中，∠C=90°，F、D是BC上两点，E是AF延长线上一点，∠B=∠1，∠E=∠2，BF=kDE．试探究AB、BC、DE之间的数量关系．（用含有k的代数式表示）
如图所示，用一根长为60cm的铁丝折成由两个小矩形组成的大矩形，设大矩形的一边长为x cm．