题目内容
15.函数y=6x2的图象开口方向为向上,顶点坐标是(0,0),对称轴是x=0,图象有最低(填“最高”或“最低”)点,函数有最小值,当x>0时,y随x的增大而增大.分析 利用二次函数的性质,利用开口方向,最值,开口程度以及函数的增减性逐一探讨得出答案即可.
解答 解:y=6x2的图象开口方向为向上,顶点坐标是(0,0),对称轴是x=0,图象有最低点,函数有最小值,当x>0时,y随x的增大而增大.
故答案为:向上,(0,0),x=0,最低,小,增大.
点评 本题考查了二次函数的性质:二次函数y=ax2+bx+c(a≠0)的顶点坐标是(-$\frac{b}{2a}$,$\frac{4ac-{b}^{2}}{4a}$),对称轴直线x=-$\frac{b}{2a}$,二次函数y=ax2+bx+c(a≠0)的图象具有如下性质:当a>0时,抛物线y=ax2+bx+c(a≠0)的开口向上,x<-$\frac{b}{2a}$时,y随x的增大而减小;x>-$\frac{b}{2a}$时,y随x的增大而增大;x=-$\frac{b}{2a}$时,y取得最小值$\frac{4ac-{b}^{2}}{4a}$,即顶点是抛物线的最低点;当a<0时,抛物线y=ax2+bx+c(a≠0)的开口向下,x<-$\frac{b}{2a}$时,y随x的增大而增大;x>-$\frac{b}{2a}$时,y随x的增大而减小;x=-$\frac{b}{2a}$时,y取得最大值$\frac{4ac-{b}^{2}}{4a}$,即顶点是抛物线的最高点.

练习册系列答案
 快乐5加2金卷系列答案
快乐5加2金卷系列答案
相关题目
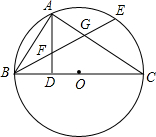 如图,BC是⊙O的直径,点A在⊙O上,AD⊥BC,垂足为D,$\widehat{AE}$=$\widehat{AB}$,BE分别交AD、AC于点F、G,判断△FAG的形状,并说明理由.
如图,BC是⊙O的直径,点A在⊙O上,AD⊥BC,垂足为D,$\widehat{AE}$=$\widehat{AB}$,BE分别交AD、AC于点F、G,判断△FAG的形状,并说明理由.