题目内容
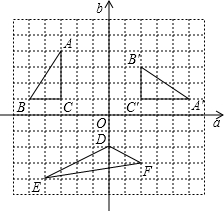 在如图所示的方格纸中,把每个小正方形的顶点称为“格点”,以格点为顶点的三角形叫做“格点三角形”.根据图形,解决下面的问题:
在如图所示的方格纸中,把每个小正方形的顶点称为“格点”,以格点为顶点的三角形叫做“格点三角形”.根据图形,解决下面的问题:(1)请描述图中的格点△A′B′C′是由格点△ABC通过哪些变换方式得到的?
(2)若以直线a,b为坐标轴建立平面直角坐标系后,点C的坐标为(-3,1),请写出格点△DEF各顶点的坐标,并求出△DEF的面积.
考点:作图-旋转变换,作图-平移变换
专题:作图题
分析:(1)根据两个三角形的对应点的关系以及旋转、平移的性质解答;
(2)根据平面直角坐标系写出点D、E、F的坐标即可,再根据△DEF的面积等于三角形所在的矩形的面积减去四周桑直角三角形的面积列式计算即可得解.
(2)根据平面直角坐标系写出点D、E、F的坐标即可,再根据△DEF的面积等于三角形所在的矩形的面积减去四周桑直角三角形的面积列式计算即可得解.
解答:解:(1)先将△ABC绕点C按顺时针方向旋转90°,再向右平移5个单位得到△A′B′C′(或先平移再旋转也可);
(2)D(0,-2),E(-4,-4),F(2,-3).
S△DEF=6×2-
×4×2-
×2×1-
×6×1=4.
(2)D(0,-2),E(-4,-4),F(2,-3).
S△DEF=6×2-
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
点评:本题考查了利用旋转变换,平移变化作图,在平面直角坐标系中,图形的平移、对称、旋转等变换会引起坐标的变化,同样,坐标的变化也会引起图形的变换,两者紧密结合充分体现了数形结合的思想.

练习册系列答案
相关题目
 如图是一块长方形ABCD的场地,长AB=a米,宽AD=b米,从A、B两处入口的小路宽都为1米,两小路汇合处路宽为2米,其余部分种植草坪,则草坪面积为
如图是一块长方形ABCD的场地,长AB=a米,宽AD=b米,从A、B两处入口的小路宽都为1米,两小路汇合处路宽为2米,其余部分种植草坪,则草坪面积为 如图,在每个小正方形边长为1的方格纸中,△ABC的顶点都在方格纸格点上.将△ABC向左平移2格,再向上平移4格.
如图,在每个小正方形边长为1的方格纸中,△ABC的顶点都在方格纸格点上.将△ABC向左平移2格,再向上平移4格.