题目内容
化简
（1）x（x-4）=5-8x；
（2）
+
-（
-
）．
（1）x（x-4）=5-8x；
（2）
| 0.5 |
| 12 |
|
4
|
考点：解一元二次方程-因式分解法,二次根式的加减法
专题：计算题
分析：（1）先把方程整理为一般式，然后利用因式分解法求解；
（2）先把各二次根式化为最简二次根式，然后合并即可．
（2）先把各二次根式化为最简二次根式，然后合并即可．
解答：解：（1）x2+4x-5=0，
（x+5）（x-1）=0，
x+5=0或x-1=0，
所以x1=-5，x2=1；
（2）原式=
+2
-
+2
=
+
．
（x+5）（x-1）=0，
x+5=0或x-1=0，
所以x1=-5，x2=1；
（2）原式=
| ||
| 2 |
| 3 |
| ||
| 3 |
| 2 |
=
5
| ||
| 2 |
5
| ||
| 3 |
点评：本题考查了解一元二次方程-因式分解法：先把方程的右边化为0，再把左边通过因式分解化为两个一次因式的积的形式，那么这两个因式的值就都有可能为0，这就能得到两个一元一次方程的解，这样也就把原方程进行了降次，把解一元二次方程转化为解一元一次方程的问题了（数学转化思想）．也考查了二次根式的加减运算．
练习册系列答案
名校课堂系列答案
相关题目
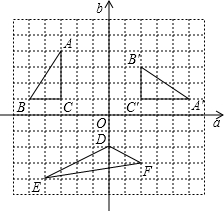在如图所示的方格纸中，把每个小正方形的顶点称为“格点”，以格点为顶点的三角形叫做“格点三角形”．根据图形，解决下面的问题：