题目内容
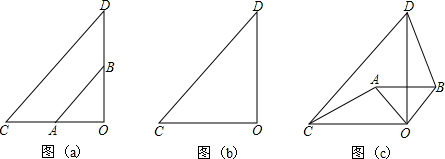
如图(a),两个不全等的等腰直角三角形OAB和OCD叠放在一起,并且有公共的直角顶点O.
(1)将图(a)中的△OAB绕点O顺时针旋转90°角,在图(b)中作出旋转后的△OAB(保留作图痕迹,不写作法,不证明);
(2)在图(b)中,试探究线段AC与线段BD的关系,并说明理由;
(3)将图(a)中的△OAB绕点O顺时针旋转一个锐角,得到图(c),这时(2)中的结论是否仍成立?请作出判断并说明理由.
(1)将图(a)中的△OAB绕点O顺时针旋转90°角,在图(b)中作出旋转后的△OAB(保留作图痕迹,不写作法,不证明);
(2)在图(b)中,试探究线段AC与线段BD的关系,并说明理由;
(3)将图(a)中的△OAB绕点O顺时针旋转一个锐角,得到图(c),这时(2)中的结论是否仍成立?请作出判断并说明理由.

考点:全等三角形的判定与性质,等腰直角三角形,旋转的性质
专题:
分析:(1)△OAB绕点O顺时针旋转90°角应该在△COD的右边;
(2)的结论容易得到,AC=BD,AC与BD相交成90°的角;
(3)结论仍然成立,利用等腰直角三角形的性质可以得到全等条件证明△COA≌△DOB,然后利用全等三角形的性质可以证明结论仍然成立.
(2)的结论容易得到,AC=BD,AC与BD相交成90°的角;
(3)结论仍然成立,利用等腰直角三角形的性质可以得到全等条件证明△COA≌△DOB,然后利用全等三角形的性质可以证明结论仍然成立.
解答: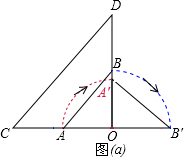 解:(1)如图(a)所示:△A′OB′即为所求的三角形;
解:(1)如图(a)所示:△A′OB′即为所求的三角形;
(2)数量关系:AC=BD,位置关系:AC⊥BD.
如图(b),连接AC、BD,延长CA交BD于点F;
∵△AOC与△BOD中,
,
∴△AOC≌△BOD(SAS),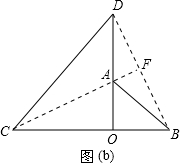
∴∠ACO=∠BDO,AC=BD.
∵∠ACO+∠CAO=90°,∠CAO=∠DAF
∴∠BDO+∠DAF=90°,
∴AF⊥DF,即AC⊥BD;
(3)结论仍然成立.
理由:如图(c),延长CA交DO于点E,交BD于点G.
∵△AOC与△BOD中,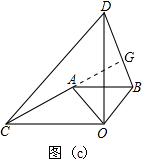
,
∴△AOC≌△BOD(SAS),
∴AC=BD,∠ACO=∠BDO
∵∠ECO+∠CEO=90°,∠DEG=∠CEO
∴∠GDE+∠DEG=90°,
∴∠DGE=90°,
∴AC⊥BD.
 解:(1)如图(a)所示:△A′OB′即为所求的三角形;
解:(1)如图(a)所示:△A′OB′即为所求的三角形;(2)数量关系:AC=BD,位置关系:AC⊥BD.
如图(b),连接AC、BD,延长CA交BD于点F;
∵△AOC与△BOD中,
|
∴△AOC≌△BOD(SAS),

∴∠ACO=∠BDO,AC=BD.
∵∠ACO+∠CAO=90°,∠CAO=∠DAF
∴∠BDO+∠DAF=90°,
∴AF⊥DF,即AC⊥BD;
(3)结论仍然成立.
理由:如图(c),延长CA交DO于点E,交BD于点G.
∵△AOC与△BOD中,

|
∴△AOC≌△BOD(SAS),
∴AC=BD,∠ACO=∠BDO
∵∠ECO+∠CEO=90°,∠DEG=∠CEO
∴∠GDE+∠DEG=90°,
∴∠DGE=90°,
∴AC⊥BD.
点评:本题考查了图形的旋转变化,学生要看清是顺时针还是逆时针旋转,然后画出图形,利用图形的性质通过证明三角形全等就可以解决问题.

练习册系列答案
 学练快车道快乐假期寒假作业系列答案
学练快车道快乐假期寒假作业系列答案
相关题目
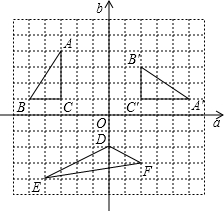 在如图所示的方格纸中,把每个小正方形的顶点称为“格点”,以格点为顶点的三角形叫做“格点三角形”.根据图形,解决下面的问题:
在如图所示的方格纸中,把每个小正方形的顶点称为“格点”,以格点为顶点的三角形叫做“格点三角形”.根据图形,解决下面的问题:
 如图,在△ABC中,M在BC上,D在AM上,AB=AC,DB=DC.
如图,在△ABC中,M在BC上,D在AM上,AB=AC,DB=DC.