题目内容

6．方程组$\left\{\begin{array}{l}{x-y=4}\\{2x+y=-1}\end{array}\right.$的解是$\left\{\begin{array}{l}{x=1}\\{y=-3}\end{array}\right.$．

分析 方程组利用加减消元法求出解即可．

解答 解：$\left\{\begin{array}{l}{x-y=4①}\\{2x+y=-1②}\end{array}\right.$，
①+②得：3x=3，即x=1，
把x=1代入①得：y=-3，
则方程组的解为$\left\{\begin{array}{l}{x=1}\\{y=-3}\end{array}\right.$，
故答案为：$\left\{\begin{array}{l}{x=1}\\{y=-3}\end{array}\right.$

点评 此题考查了解二元一次方程组，利用了消元的思想，消元的方法有：代入消元法与加减消元法．

练习册系列答案
相关题目
16．解不等式组$\left\{\begin{array}{l}{\frac{1}{2}x＞1①}\\{1-x≥-3②}\end{array}\right.$
请结合题意，完成本题解答．
（Ⅰ）解不等式①，得x＞2；
（Ⅱ）解不等式②，得x≤4；
（Ⅲ）把不等式①和②的解集在数轴上表示出来：

（Ⅳ）原不等式组的解集为2＜x≤4．
17．随着服装市场竞争日益激烈，某品牌服装专卖店一款服装按原售价降价a元后，再次降价20%，现售价为b元，则原售价为（　　）
A．（a+$\frac{5}{4}$b）元B．（a+$\frac{4}{5}$b）元C．（b+$\frac{5}{4}$a）元D．（b+$\frac{4}{5}$a）元
14．如图，在⊙O中，AB为直径，CD为弦，已知∠ACD=40°，则∠BAD=50度．
1．计算：（ab2）3=（　　）
A．3ab2B．ab6C．a3b6D．a3b2
11．东营市出租车的收费标准是：起步价8元（即行驶距离不超过3千米都需付8元车费），超过3千米以后，每增加1千米，加收1.5元（不足1千米按1千米计）．某人从甲地到乙地经过的路程是x千米，出租车费为15.5元，那么x的最大值是（　　）
A．11B．8C．7D．5
18．若分式方程$\frac{x-a}{x+1}$=a无解，则a的值为1或-1．
5．如图，已知，A（0，4），B（-3，0），C（2，0），D为B点关于AC的对称点，反比例函数y=$\frac{k}{x}$的图象经过D点．
（1）证明四边形ABCD为菱形；
（2）求此反比例函数的解析式；
（3）已知在y=$\frac{k}{x}$的图象（x＞0）上一点N，y轴正半轴上一点M，且四边形ABMN是平行四边形，求M点的坐标．
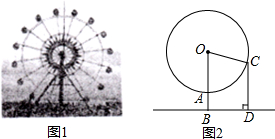6．图1是某游乐场的摩天轮，图2是它的正面示意图，已知摩天轮的半径为40米，每分钟绕圆心O匀速旋转15°，其最低点A离地面的距离AB为5米，小明从点A处登上摩天轮，5分钟后旋转到点C，此时小明绕点O旋转了多少度？他离地面的高度CD是多少米？（结果精确到0.1米）

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网