题目内容
10. 如图,矩形ABCD的外接圆O与水平地面相切于点A,已知圆O的半径为4,且$\widehat{BC}$=2$\widehat{AB}$.若在没有滑动的情况下,将圆O向右滚动,使得O点向右移动了66π,则此时与地面相切的弧为( )
如图,矩形ABCD的外接圆O与水平地面相切于点A,已知圆O的半径为4,且$\widehat{BC}$=2$\widehat{AB}$.若在没有滑动的情况下,将圆O向右滚动,使得O点向右移动了66π,则此时与地面相切的弧为( )| A. | $\widehat{AB}$ | B. | $\widehat{BC}$ | C. | $\widehat{CD}$ | D. | $\widehat{DA}$ |
分析 根据圆的周长公式求出圆的周长以及圆转动的周数,根据题意分别求出$\widehat{AB}$和$\widehat{AB}$+$\widehat{BC}$的长,比较即可得到答案.
解答 解:∵圆O半径为4,
∴圆的周长为:2π×r=8π,
∵将圆O向右滚动,使得O点向右移动了66π,
∴66π÷8π=8…2π,
即圆滚动8周后,又向右滚动了2π,
∵矩形ABCD的外接圆O与水平地面相切于A点,$\widehat{BC}$=2$\widehat{AB}$,
∴$\widehat{AB}$=$\frac{1}{6}$×8π=$\frac{4}{3}π$<2π,$\widehat{AB}$+$\widehat{CB}$=$\frac{1}{2}×$8π=4π>2π,
∴此时与地面相切的弧为$\widehat{BC}$,
故选:B.
点评 此题主要考查了旋转的性质以及圆的周长公式等知识,得出O点转动的周数是解题关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
20.已知直角三角形的两条直角边的长分别为$\sqrt{3}$和$\sqrt{6}$,则这个直角三角形的面积为( )
| A. | $\sqrt{18}$ | B. | 2$\sqrt{18}$ | C. | $\frac{3}{2}$$\sqrt{2}$ | D. | 18 |
18.对于实数a、b,定义一种运算“?”为:a?b=a2+ab-2,有下列命题:
①1?3=2;②方程x?1=0的根为:x1=-2,x2=1;③不等式组$\left\{\begin{array}{l}{(-2)?x-4<0}\\{1?x-3<0}\end{array}\right.$的解集为:-1<x<4;④点(1,-2)在函数y=x?(-1)的图象上.
其中正确的是( )
①1?3=2;②方程x?1=0的根为:x1=-2,x2=1;③不等式组$\left\{\begin{array}{l}{(-2)?x-4<0}\\{1?x-3<0}\end{array}\right.$的解集为:-1<x<4;④点(1,-2)在函数y=x?(-1)的图象上.
其中正确的是( )
| A. | ①②③④ | B. | ①③④ | C. | ①②④ | D. | ①②③ |
5.下列变形正确的是( )
| A. | (a2)3=a9 | B. | 2a×3a=6a2 | C. | a6-a2=a4 | D. | 2a+3b=6ab |
19.气温由-2℃上升3℃后是( )
| A. | -5℃ | B. | 1℃ | C. | 5℃ | D. | 3℃ |
20.下列函数的图象中,有最低点的函数是( )
| A. | y=-4x2 | B. | y=-2x+3 | C. | y=3x+5 | D. | y=$\frac{1}{4}$x2 |
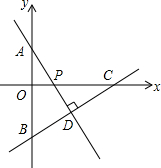 如图,在平面直角坐标系中,已知A,B两点的坐标分别是(0,2),0,-3),点P是x轴正半轴上一个动点,过点B作直线BC⊥AP于点D,直线BC与x轴交于点C.
如图,在平面直角坐标系中,已知A,B两点的坐标分别是(0,2),0,-3),点P是x轴正半轴上一个动点,过点B作直线BC⊥AP于点D,直线BC与x轴交于点C.