题目内容
7.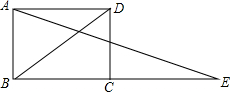 如图,在矩形ABCD中,AB=2,AD=2$\sqrt{3}$,点E在BC的延长线上,且BD=CE,连接AE,则∠E的度数为( )
如图,在矩形ABCD中,AB=2,AD=2$\sqrt{3}$,点E在BC的延长线上,且BD=CE,连接AE,则∠E的度数为( )| A. | 15° | B. | 20° | C. | 30° | D. | 45° |
分析 由矩形的性质得出BC=AD=2$\sqrt{3}$,AC=BD,∠ABC=90°,由勾股定理求出AC,得出AC,求出AB=$\frac{1}{2}$AC,得出∠ACB=30°,求出AC=CE,由等腰三角形的性质得出∠E=∠CAE,再由三角形的外角性质即可得出∠E=15°.
解答 解:连接AC,如图所示:
∵四边形ABCD是矩形,
∴BC=AD=2$\sqrt{3}$,AC=BD,∠ABC=90°,
∴AC=$\sqrt{A{B}^{2}+B{C}^{2}}$=$\sqrt{{2}^{2}+(2\sqrt{3})^{2}}$=4,
∴AB=$\frac{1}{2}$AC,
∴∠ACB=30°,
∵BD=CE,
∴AC=CE,
∴∠E=∠CAE,
∵∠ACB=∠E+∠CAE,
∴∠E=15°;
故选:A.
点评 本题考查了矩形的性质、勾股定理、等腰三角形的性质、含30°角的直角三角形的判定等知识;熟练掌握矩形的性质,求出∠ACB=30°是解决问题的突破口.

练习册系列答案
相关题目
17.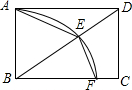 如图,在矩形ABCD中,以点B为圆心,AB长为半径画弧,交对角线BD于点E,交BC于点F,连接AE,EF.若∠BEF=70°,则∠DAE的度数是( )
如图,在矩形ABCD中,以点B为圆心,AB长为半径画弧,交对角线BD于点E,交BC于点F,连接AE,EF.若∠BEF=70°,则∠DAE的度数是( )
 如图,在矩形ABCD中,以点B为圆心,AB长为半径画弧,交对角线BD于点E,交BC于点F,连接AE,EF.若∠BEF=70°,则∠DAE的度数是( )
如图,在矩形ABCD中,以点B为圆心,AB长为半径画弧,交对角线BD于点E,交BC于点F,连接AE,EF.若∠BEF=70°,则∠DAE的度数是( )| A. | 10° | B. | 20° | C. | 25° | D. | 30° |
18.对于实数a、b,定义一种运算“?”为:a?b=a2+ab-2,有下列命题:
①1?3=2;②方程x?1=0的根为:x1=-2,x2=1;③不等式组$\left\{\begin{array}{l}{(-2)?x-4<0}\\{1?x-3<0}\end{array}\right.$的解集为:-1<x<4;④点(1,-2)在函数y=x?(-1)的图象上.
其中正确的是( )
①1?3=2;②方程x?1=0的根为:x1=-2,x2=1;③不等式组$\left\{\begin{array}{l}{(-2)?x-4<0}\\{1?x-3<0}\end{array}\right.$的解集为:-1<x<4;④点(1,-2)在函数y=x?(-1)的图象上.
其中正确的是( )
| A. | ①②③④ | B. | ①③④ | C. | ①②④ | D. | ①②③ |
12.下列运算正确的是( )
| A. | $\sqrt{9}$=±3 | B. | $\root{3}{4}$=2 | ||
| C. | (x+2y)2=x2+2xy+4y2 | D. | $\sqrt{18}$-$\sqrt{8}$=$\sqrt{2}$ |
19.气温由-2℃上升3℃后是( )
| A. | -5℃ | B. | 1℃ | C. | 5℃ | D. | 3℃ |
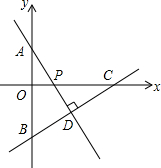 如图,在平面直角坐标系中,已知A,B两点的坐标分别是(0,2),0,-3),点P是x轴正半轴上一个动点,过点B作直线BC⊥AP于点D,直线BC与x轴交于点C.
如图,在平面直角坐标系中,已知A,B两点的坐标分别是(0,2),0,-3),点P是x轴正半轴上一个动点,过点B作直线BC⊥AP于点D,直线BC与x轴交于点C.