题目内容
 如图,等边△ABC中,点D在延长线上,CE平分∠ACD,且CE=BD.
如图,等边△ABC中,点D在延长线上,CE平分∠ACD,且CE=BD.说明:△ADE是等边三角形.
考点:等边三角形的判定与性质
专题:证明题
分析:由条件可以容易证明△ABD≌△ACE,进一步得出AD=AE,∠BAD=∠CAE,加上∠DAE=60°,即可证明△ADE为等边三角形.
解答:证明:∵△ABC为等边三角形,
∴∠B=∠ACB=60°,AB=AC,
即∠ACD=120°,
∵CE平分∠ACD,
∴∠ACE=∠DCE=60°,
在△ABD和△ACE中,
,
∴△ABD≌△ACE(SAS),
∴AD=AE,∠BAD=∠CAE,
又∵∠BAC=60°,
∴∠DAE=60°,
∴△ADE为等边三角形.
∴∠B=∠ACB=60°,AB=AC,
即∠ACD=120°,
∵CE平分∠ACD,
∴∠ACE=∠DCE=60°,
在△ABD和△ACE中,
|
∴△ABD≌△ACE(SAS),
∴AD=AE,∠BAD=∠CAE,
又∵∠BAC=60°,
∴∠DAE=60°,
∴△ADE为等边三角形.
点评:本题考查了等边三角形的判定与性质,难度适中,关键找出判定三角形等边的条件.

练习册系列答案
相关题目
设a>0,b>0,c>0,且
+
+
=3,则以下说法正确的是( )
| b |
| a |
| c |
| b |
| a |
| c |
| A、a,b,c可能相等,也可能不等 |
| B、a,b,c相等 |
| C、a,b,c不相等 |
| D、以上说法都不对 |
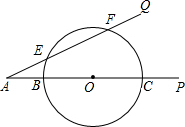 已知:如图,∠PAQ=30°,在边AP上顺次截取AB=3cm,BC=10cm,以BC为直径作⊙O交射线AQ于E、F两点,求:
已知:如图,∠PAQ=30°,在边AP上顺次截取AB=3cm,BC=10cm,以BC为直径作⊙O交射线AQ于E、F两点,求: 某商店第一次用600元购进某种型号的铅笔若干支,第二次又用600元购进该款铅笔,但这次每支的进价比第一次贵1元,所以购进数量比第一次少了30支.
某商店第一次用600元购进某种型号的铅笔若干支,第二次又用600元购进该款铅笔,但这次每支的进价比第一次贵1元,所以购进数量比第一次少了30支. 如图,在图1中,AB是圆的直径,点P是根据圆的相关性质用无刻度的直尺画出的△ABC三条高的交点;依据图1给你的作法启示,请你在图2中,先用尺规画出以AB为直径的⊙0,然后仅用无刻度的直尺画出△ABC中AB边上的高CD.(要求:不写作法,保留作图痕迹,写出结论.)
如图,在图1中,AB是圆的直径,点P是根据圆的相关性质用无刻度的直尺画出的△ABC三条高的交点;依据图1给你的作法启示,请你在图2中,先用尺规画出以AB为直径的⊙0,然后仅用无刻度的直尺画出△ABC中AB边上的高CD.(要求:不写作法,保留作图痕迹,写出结论.)