题目内容
设a>0,b>0,c>0,且
+
+
=3,则以下说法正确的是( )
| b |
| a |
| c |
| b |
| a |
| c |
| A、a,b,c可能相等,也可能不等 |
| B、a,b,c相等 |
| C、a,b,c不相等 |
| D、以上说法都不对 |
考点:拆项、添项、配方、待定系数法
专题:
分析:设
=x3,
=y3,
=z3,则x3y3z3=
•
•
=1,即xyz=1,再根据a>0,b>0,c>0得出x>0,y>0,z>0,故可得出x、y、z的关系,进而得出
=
=
,由此可得出结论.
| b |
| a |
| c |
| b |
| a |
| c |
| b |
| a |
| c |
| b |
| a |
| c |
| b |
| a |
| c |
| b |
| a |
| c |
解答:解:设
=x3,
=y3,
=z3,则x3y3z3=
•
•
=1,即xyz=1,
由已知可得:x3+y3+z3-3xyz=0,
即(x+y+z)(x2+y2+z2-xy-xz-yz)=0
∵a>0,b>0,c>0,
∴x>0,y>0,z>0,
∴x+y+z>0
∴x2+y2+z2-xy-xz-yz=0,即:x=y=z
∴
=
=
,即a2=bc,b2=ac,c2=ab,
由a2=bc,b2=ac,得a=b
由b2=ac,c2=ab得b=c
∴a=b=c
故选B.
| b |
| a |
| c |
| b |
| a |
| c |
| b |
| a |
| c |
| b |
| a |
| c |
由已知可得:x3+y3+z3-3xyz=0,
即(x+y+z)(x2+y2+z2-xy-xz-yz)=0
∵a>0,b>0,c>0,
∴x>0,y>0,z>0,
∴x+y+z>0
∴x2+y2+z2-xy-xz-yz=0,即:x=y=z
∴
| b |
| a |
| c |
| b |
| a |
| c |
由a2=bc,b2=ac,得a=b
由b2=ac,c2=ab得b=c
∴a=b=c
故选B.
点评:本题考查的是拆项、添项、配方及待定系数法,此题中先根据题意得出x、y、z的关系是解答此题的关键.

练习册系列答案
 寒假学与练系列答案
寒假学与练系列答案
相关题目
(-
×103)2×(1.5×104)2的计算结果是( )
| 2 |
| 3 |
| A、-1.5×1011 | ||
B、
| ||
| C、1014 | ||
| D、-1014 |
四边形ABCD为菱形,AC、BD为对角线,若AC=6,BD=8,则sin∠ABD的值为( )
A、
| ||
B、
| ||
C、
| ||
D、
|
从1999年11月1日起,全国储蓄存款征收利息税,税率是利息的20%,即储蓄利息的20%由各银行储蓄点代扣代收,小明的爸爸在2013年4月存入人民币若干元,年利率为2.25%,一年到期后将缴纳利息税72元,则小明的爸爸存入的人民币为( )
| A、1600元 |
| B、16000元 |
| C、360元 |
| D、3600元 |
已知OA⊥OB,∠AOB:∠AOC=3:4,则∠BOC的度数为( )
| A、30° |
| B、150° |
| C、30°或150° |
| D、不同于以上答案 |
 如图,一个有进水管与出水管的容器,从某时刻开始的4分钟内只进水不出水,在随后的8 分钟内既进水又出水,每分的进水量和出水量是两个常数,容器内的水量y(单位:升)与时间x(单位:分钟)之间的关系如图所示.则下列说法正确的个数是( )
如图,一个有进水管与出水管的容器,从某时刻开始的4分钟内只进水不出水,在随后的8 分钟内既进水又出水,每分的进水量和出水量是两个常数,容器内的水量y(单位:升)与时间x(单位:分钟)之间的关系如图所示.则下列说法正确的个数是( )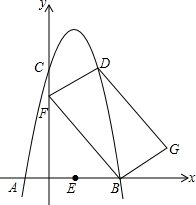 如图,抛物线经过A,C,D三点,且三点坐标为A(-1,0),C(0,5),D(2,5),抛物线与x轴的另一个交点为B点,点F为y轴上一动点,作平行四边形DFBG,
如图,抛物线经过A,C,D三点,且三点坐标为A(-1,0),C(0,5),D(2,5),抛物线与x轴的另一个交点为B点,点F为y轴上一动点,作平行四边形DFBG, 如图,等边△ABC中,点D在延长线上,CE平分∠ACD,且CE=BD.
如图,等边△ABC中,点D在延长线上,CE平分∠ACD,且CE=BD.