题目内容
3.在?ABCD中,∠ABC=30°,AE⊥BC于E,AF⊥CD于F,已知BE=$\sqrt{3}$,CF=1,则AC=$\frac{2\sqrt{3}}{3}$ 或2.分析 分两种情形:①如图1中,当F在线段CD上时.②当F在线段DC的延长线上时,分别求解即可.
解答 解:①如图1中,当F在线段CD上时.
在Rt△ABE中,∵∠B=30°,BE=$\sqrt{3}$,∠AEB=90°,
∴AE=1,AB=2,
∵CF=1,AB=CD=2,
∴DF=CF=1,
∵AF⊥CD,
∴AC=AD,
在Rt△ADF中,∠D=30°,cos30°=$\frac{DF}{AD}$,
∴AD=$\frac{2\sqrt{3}}{3}$,
∴AC=$\frac{2\sqrt{3}}{3}$,
②当F在线段DC的延长线上时,
在Rt△ABE中,∵∠B=30°,BE=$\sqrt{3}$,∠AEB=90°,
∴AE=1,AB=2,
∵CF=1,AB=CD=2,
∴DF=3,
∵AF⊥CD,∠D=∠B=30°,
∴AD=BC=2$\sqrt{3}$,
∴BE=EC,
∵AE⊥BC,
∴AC=AB=2,
故答案为$\frac{2\sqrt{3}}{3}$或2
点评 本题看平行四边形的性质、解直角三角形、锐角三角函数等知识,解题的关键是学会用分类讨论的思想思考问题,则有一题多解,属于中考填空题中的压轴题.

练习册系列答案
 轻松课堂单元测试AB卷系列答案
轻松课堂单元测试AB卷系列答案 小题狂做系列答案
小题狂做系列答案
相关题目
8.交换下列命题的题设和结论,得到的新命题是假命题的是( )
| A. | 两直线平行,同位角相等 | B. | 相等的角是对顶角 | ||
| C. | 所有的直角都是相等的 | D. | 若a=b,则a-3=b-3 |
15.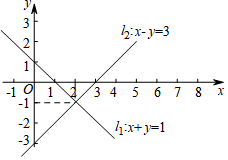 如图,在平面直角坐标系中,二元一次方程x+y=1和x-y=3的图象分别是直线l1和l2.则方程组$\left\{\begin{array}{l}{x+y=1}\\{x-y=3}\end{array}\right.$的解是( )
如图,在平面直角坐标系中,二元一次方程x+y=1和x-y=3的图象分别是直线l1和l2.则方程组$\left\{\begin{array}{l}{x+y=1}\\{x-y=3}\end{array}\right.$的解是( )
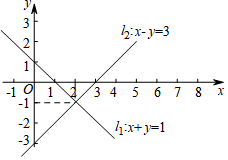 如图,在平面直角坐标系中,二元一次方程x+y=1和x-y=3的图象分别是直线l1和l2.则方程组$\left\{\begin{array}{l}{x+y=1}\\{x-y=3}\end{array}\right.$的解是( )
如图,在平面直角坐标系中,二元一次方程x+y=1和x-y=3的图象分别是直线l1和l2.则方程组$\left\{\begin{array}{l}{x+y=1}\\{x-y=3}\end{array}\right.$的解是( )| A. | $\left\{\begin{array}{l}{x=2}\\{y=-1}\end{array}\right.$ | B. | $\left\{\begin{array}{l}{x=-1}\\{y=2}\end{array}\right.$ | C. | $\left\{\begin{array}{l}{x=-2}\\{y=1}\end{array}\right.$ | D. | $\left\{\begin{array}{l}{x=1}\\{y=-2}\end{array}\right.$ |
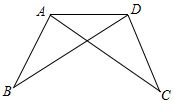 如图,AB=DC,若证明△ABD≌△DCA,可以补充的一个条件是∠BAD=∠CDA.
如图,AB=DC,若证明△ABD≌△DCA,可以补充的一个条件是∠BAD=∠CDA.