题目内容
当m____时,函数y=(m-2)x2+4x-5(m是常数)是二次函数.
 ≠2
【解析】根据二次函数的概念,可知m-2≠0,解得m≠2.
故答案为:≠2.
≠2
【解析】根据二次函数的概念,可知m-2≠0,解得m≠2.
故答案为:≠2.
练习册系列答案
相关题目
已知二次函数y=﹣x2+2x+m的部分图象如图所示,则关于x的一元二次方程﹣x2+2x+m=0的解为_____.

 x1=4,x2=﹣2
【解析】试题分析:由二次函数y=﹣x2+2x+m的部分图象可以得到抛物线的对称轴和抛物线与x轴的一个交点坐标,然后可以求出另一个交点坐标,再利用抛物线与x轴交点的横坐标与相应的一元二次方程的根的关系即可得到关于x的一元二次方程﹣x2+2x+m=0的解.
【解析】
依题意得二次函数y=﹣x2+2x+m的对称轴为x=1,与x轴的一个交点为(3,0),
∴抛物线...
x1=4,x2=﹣2
【解析】试题分析:由二次函数y=﹣x2+2x+m的部分图象可以得到抛物线的对称轴和抛物线与x轴的一个交点坐标,然后可以求出另一个交点坐标,再利用抛物线与x轴交点的横坐标与相应的一元二次方程的根的关系即可得到关于x的一元二次方程﹣x2+2x+m=0的解.
【解析】
依题意得二次函数y=﹣x2+2x+m的对称轴为x=1,与x轴的一个交点为(3,0),
∴抛物线... 如图,当小杰沿坡度i=1:5的坡面由B到A行走了26米时,小杰实际上升高度AC=_________米.(可以用根号表示)

 【解析】试题分析:根据坡度的定义可设AC=x,BC=5x,再根据勾股定理即可列方程求解.
由题意设AC=x,BC=5x,则,解得,
则小杰实际上升高度米.
【解析】试题分析:根据坡度的定义可设AC=x,BC=5x,再根据勾股定理即可列方程求解.
由题意设AC=x,BC=5x,则,解得,
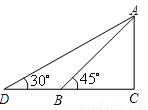
则小杰实际上升高度米. 如图,为安全起见,萌萌拟加长滑梯,将其倾斜角由45°降至30°.已知滑梯AB的长为3m,点D、B、C在同一水平地面上,那么加长后的滑梯AD的长是( )
A. 2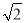 B.
B. 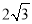 C.
C. 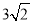 D.
D. 
 C
【解析】试题分析:根据AB的长度以及△ABC的三角函数可得:AC=米,根据Rt△ADC中∠D的正弦值可得:AD=2AC=米,故选C.
C
【解析】试题分析:根据AB的长度以及△ABC的三角函数可得:AC=米,根据Rt△ADC中∠D的正弦值可得:AD=2AC=米,故选C. 如图,对称轴平行于y轴的抛物线与x轴交于(1,0)、(3,0)两点,则它的对称轴为____________________.
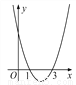
 直线x=2
【解析】试题分析:当两点到对称轴距离相等时,则所对应的函数值相等,则二次函数的对称轴为:x==2.
直线x=2
【解析】试题分析:当两点到对称轴距离相等时,则所对应的函数值相等,则二次函数的对称轴为:x==2. 在二次函数①y=3x2;②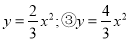 中,图象在同一水平线上的开口大小顺序用题号表示应该为( )
中,图象在同一水平线上的开口大小顺序用题号表示应该为( )
A. ①>②>③ B. ①>③>②
C. ②>③>① D. ②>①>③
 C
【解析】根据二次函数的性质,可知系数a决定开口方向和开口大小,且a的值越大开口越小,因此可知②>③>①.
故选:C.
C
【解析】根据二次函数的性质,可知系数a决定开口方向和开口大小,且a的值越大开口越小,因此可知②>③>①.
故选:C. 分解因式: 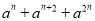 =_______.
=_______.
 【解析】提取公因式分解因式即可,即原式=.
【解析】提取公因式分解因式即可,即原式=. 已知x2-2x-3=0,则代数式6-2x2+4x的值是多少?
 0.
【解析】试题分析:已知x2-2x-3=0,可得x2-2x=3,把代数式6-2x2+4x化为6-2(x2-2x),代入求值即可.
试题解析:
∵x2-2x-3=0,
∴x2-2x=3,
∴6-2x2+4x=6-2(x2-2x)=6-2×3=0.
0.
【解析】试题分析:已知x2-2x-3=0,可得x2-2x=3,把代数式6-2x2+4x化为6-2(x2-2x),代入求值即可.
试题解析:
∵x2-2x-3=0,
∴x2-2x=3,
∴6-2x2+4x=6-2(x2-2x)=6-2×3=0. (8分)在平面直角坐标系xOy中,抛物线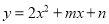 经过点A(0,-2),B(3,4).
经过点A(0,-2),B(3,4).
(1)求抛物线的表达式及对称轴;
(2)设点B关于原点的对称点为C,点D是抛物线对称轴上一动点,记抛物线在A,B之间的部分为图像G(包含A,B两点).若直线CD与图像G有公共点,结合函数图像,求点D纵坐标t 的取值范围.
 (1), (2)
【解析】试题分析:利用待定系数法求得解析式,再根据对称轴公式x=求得对称轴;画出图像找到D点的两个位置,进而求出范围.
试题解析:直线CD解析式:或y=-4
(1), (2)
【解析】试题分析:利用待定系数法求得解析式,再根据对称轴公式x=求得对称轴;画出图像找到D点的两个位置,进而求出范围.
试题解析:直线CD解析式:或y=-4 
