题目内容
分解因式：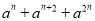 
=_______.
【解析】提取公因式分解因式即可，即原式=.
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
如图，在平面直角坐标系中，O是坐标原点，点A的坐标是(－2，4)，过点A作AB⊥y轴，垂足为B，连接OA.
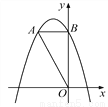
(1)求△OAB的面积；
(2)若抛物线y＝－x2－2x＋c经过点A.
①求c的值；
②将抛物线向下平移m个单位长度，使平移后得到的抛物线顶点落在△OAB的内部(不包括△OAB的边界)，求m的取值范围(直接写出答案即可)．
（1）4；（2）①c＝4；②m的取值范围为1＜m＜3.
【解析】（1）根据点A的坐标是（-2，4），得出AB，BO的长度，即可得出△OAB的面积；
（2）①把点A的坐标（-2，4）代入y=-x2-2x+c中，直接得出即可；
②利用配方法求出二次函数解析式即可得出顶点坐标，根据AB的中点E的坐标以及F点的坐标即可得出m的取值范围．
【解析】
（1）∵点A的坐标是（-2，4）... 如图是某商场一楼与二楼之间的手扶电梯示意图，其中AB、CD分别表示一楼、二楼地面的水平线，∠ABC=150°，如果顾客乘地铁从点B到点C上升的高度为5m，则电梯BC的长是（ ）
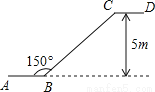
A．5cm B．5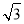
cm C．10m D．
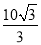m
C．
【解析】
试题分析：如图所示：过点C作CE⊥AB延长线于点E，
∵∠ABC=150°，
∴∠CBE=30°，
∵从点B到点C上升的高度为5m，
∴电梯BC的长是10m．
故选C． 当m____时，函数y＝(m－2)x2＋4x－5(m是常数)是二次函数．
≠2
【解析】根据二次函数的概念，可知m-2≠0，解得m≠2.
故答案为：≠2. 课外拓展：不解方程组
，求
的值.
6
【解析】试题分析：把因式分解后整体代入求值即可.
试题解析：
∵x-3y=1，2x+y=6，
∴
=
=（x-3y）2（7y+2x-6y）
=（x-3y）2（y+2x），
=1×6=6. 多项式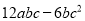
各项的公因式为（ ）
A. 2abc B.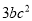 
C. 4b D. 6bc
D
【解析】多项式各项的公因式为6bc，故选D. 分解因式：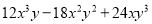 
=6xy（______）
【解析】 =6xy（）. 下列各式从左到右的变形中，是因式分解的是（ ）.
A. x（a-b）=ax-bx B. x2-1+y2=（x-1）（x+1）+y2
C. y2-1=（y+1）（y-1） D. ax+bx+c=x（a+b）+c
C
【解析】A. 是整式的乘法，故A错误；
B. 没把一个多项式转化成几个整式积，故B错误；
C. 把一个多项式转化成几个整式积，故C正确；
D. 没把一个多项式转化成几个整式积，故D错误；
故选：C. 已知抛物线的顶点坐标为P（2，-1），它的图象经过点C（0，3）．
（1）求该抛物线的解析式．
（2）设该抛物线的图象与x轴交于A、B两点，求△ABC的面积．
（1）；（2）3
【解析】分析：（1）设该抛物线方程为 ，然后将点（3，0）代入求得k的值；（2）令y=0，求出抛物线与x轴的交点坐标，然后根据三角形的面积公式列式计算求解．
本题解析：（1）∵抛物线的顶点坐标为P（2，-1），
∴设该抛物线方程为，（k≠0）；
∵它的图象经过点C（0，3），
∴，
解得k=1，
∴该抛物线的解析式为，即；
（2）令...