题目内容
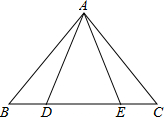 如图,已知△ABC中,AB=AC,点D、E在BC上,要使△ABD≌ACE,则只需添加一个适当的条件是
如图,已知△ABC中,AB=AC,点D、E在BC上,要使△ABD≌ACE,则只需添加一个适当的条件是考点:全等三角形的判定
专题:开放型
分析:此题是一道开放型的题目,答案不唯一,如BD=CE,根据SAS推出即可;也可以∠BAD=∠CAE等.
解答:解:BD=CE,
理由是:∵AB=AC,
∴∠B=∠C,
在△ABD和△ACE中,
,
∴△ABD≌△ACE(SAS),
故答案为:BD=CE.
理由是:∵AB=AC,
∴∠B=∠C,
在△ABD和△ACE中,
|
∴△ABD≌△ACE(SAS),
故答案为:BD=CE.
点评:本题考查了全等三角形的判定的应用,注意:全等三角形的判定定理有SAS,ASA,AAS,SSS,题目比较好,难度适中.

练习册系列答案
相关题目
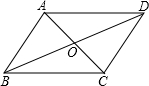 如图,在四边形ABCD中,∠DAC=∠ACB,要使四边形ABCD成为平行四边形,则应增加的条件不能是( )
如图,在四边形ABCD中,∠DAC=∠ACB,要使四边形ABCD成为平行四边形,则应增加的条件不能是( )| A、AD=BC |
| B、OA=OC |
| C、AB=CD |
| D、∠ABC+∠BCD=180° |
 如图,在等腰梯形ABCD中,AD∥BC,AB=DC,AC⊥BD.若AD=4,BC=6,则梯形ABCD的面积是
如图,在等腰梯形ABCD中,AD∥BC,AB=DC,AC⊥BD.若AD=4,BC=6,则梯形ABCD的面积是 如图,菱形ABCD的周长为16cm,BC的垂直平分线EF经过点A,则对角线BD长为
如图,菱形ABCD的周长为16cm,BC的垂直平分线EF经过点A,则对角线BD长为