题目内容
6. 如图,在△ABC中,∠C=90°,AB=30,D是AB上一点,AD:CD=25:7,且DB=DA,过AB上一点P,作PE⊥AC于E,PF⊥BD于F,则PE+PF长是18.
如图,在△ABC中,∠C=90°,AB=30,D是AB上一点,AD:CD=25:7,且DB=DA,过AB上一点P,作PE⊥AC于E,PF⊥BD于F,则PE+PF长是18.
分析 如图作AH⊥BD交BD的延长线于H,设AD=BD=25k,CD=7k,在Rt△DCB中,BC=$\sqrt{B{D}^{2}-C{D}^{2}}$=24k,在Rt△ACB中,由AC2+BC2=AB2,可得(32k)2+(24k)2=302,推出k=$\frac{3}{4}$,BC=18,由△ADH≌△BDC,推出AH=BC=18,由S△ABD=$\frac{1}{2}$•BD•AH=$\frac{1}{2}$•AD•PF+$\frac{1}{2}$•BD•PF,推出PE+PF=AH=18,
解答 解: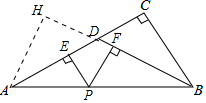 如图作AH⊥BD交BD的延长线于H,设AD=BD=25k,CD=7k,
如图作AH⊥BD交BD的延长线于H,设AD=BD=25k,CD=7k,
在Rt△DCB中,BC=$\sqrt{B{D}^{2}-C{D}^{2}}$=24k,
在Rt△ACB中,∵AC2+BC2=AB2,
∴(32k)2+(24k)2=302,
∴k=$\frac{3}{4}$,
∴BC=18,
在△ADH和△BDC中,
$\left\{\begin{array}{l}{∠ADH=∠BDC}\\{∠H=∠C=90°}\\{AD=BD}\end{array}\right.$,
∴△ADH≌△BDC,
∴AH=BC=18,
∵S△ABD=$\frac{1}{2}$•BD•AH=$\frac{1}{2}$•AD•PF+$\frac{1}{2}$•BD•PF,
∴PE+PF=AH=18,
故答案为18.
点评 本题考查勾股定理、等腰三角形的性质、全等三角形的判定和性质等知识,解题的关键是学会利用面积法证明线段之间的关系,灵活运用勾股定理解决问题,属于中考常考题型.

练习册系列答案
相关题目
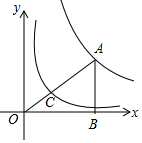 如图,已知点A在双曲线y=$\frac{9}{x}$上,AB⊥x轴于点B,连接OA交双曲线y=$\frac{k}{x}$于点C,若$\frac{OC}{CA}$=$\frac{1}{2}$,则k的值为1.
如图,已知点A在双曲线y=$\frac{9}{x}$上,AB⊥x轴于点B,连接OA交双曲线y=$\frac{k}{x}$于点C,若$\frac{OC}{CA}$=$\frac{1}{2}$,则k的值为1.
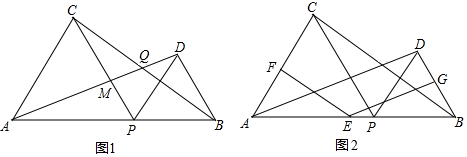
 如图,每个小正方形的边长都是1,
如图,每个小正方形的边长都是1,