题目内容
6.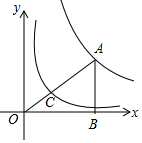 如图,已知点A在双曲线y=$\frac{9}{x}$上,AB⊥x轴于点B,连接OA交双曲线y=$\frac{k}{x}$于点C,若$\frac{OC}{CA}$=$\frac{1}{2}$,则k的值为1.
如图,已知点A在双曲线y=$\frac{9}{x}$上,AB⊥x轴于点B,连接OA交双曲线y=$\frac{k}{x}$于点C,若$\frac{OC}{CA}$=$\frac{1}{2}$,则k的值为1.
分析 过点C作CD⊥OB于点D,设C(x,y),根据相似三角形的性质得出△OCD∽△OAB,故可得出$\frac{OC}{OA}$=$\frac{CD}{AB}$=$\frac{OD}{OB}$,由$\frac{OC}{OA}$=$\frac{1}{2}$可得出$\frac{OC}{OA}$=$\frac{1}{3}$,据此可得出A点坐标,进而可得出结论.
解答  解:过点C作CD⊥OB于点D,设C(x,y),
解:过点C作CD⊥OB于点D,设C(x,y),
∵AB⊥x轴,CD⊥x轴,
∴△OCD∽△OAB,
∴$\frac{OC}{OA}$=$\frac{CD}{AB}$=$\frac{OD}{OB}$.
∵$\frac{OC}{OA}$=$\frac{1}{2}$,
∴$\frac{OC}{OA}$=$\frac{1}{3}$,
∴A(3x,3y).
∵点A在双曲线y=$\frac{9}{x}$上,
∴9xy=9,解得xy=1,
∴k=1.
点评 本题考查的是反比例函数图象上点的坐标特点,根据题意作出辅助线,构造出相似三角形是解答此题的关键.

练习册系列答案
相关题目
16.$\root{3}{64}$的算术平方根是( )
| A. | 2 | B. | -2 | C. | $\sqrt{2}$ | D. | ±$\sqrt{2}$ |
17.-|-2017|等于( )
| A. | 2017 | B. | -2017 | C. | 1 | D. | 0 |
14. 如图是一个可以自由转动的正六边形转盘,其中三个正三角形涂有阴影.转动指针,指针落在有阴影的区域内的概率为a;投掷一枚硬币,正面向上的概率为b.关于a,b大小的正确判断是( )
如图是一个可以自由转动的正六边形转盘,其中三个正三角形涂有阴影.转动指针,指针落在有阴影的区域内的概率为a;投掷一枚硬币,正面向上的概率为b.关于a,b大小的正确判断是( )
 如图是一个可以自由转动的正六边形转盘,其中三个正三角形涂有阴影.转动指针,指针落在有阴影的区域内的概率为a;投掷一枚硬币,正面向上的概率为b.关于a,b大小的正确判断是( )
如图是一个可以自由转动的正六边形转盘,其中三个正三角形涂有阴影.转动指针,指针落在有阴影的区域内的概率为a;投掷一枚硬币,正面向上的概率为b.关于a,b大小的正确判断是( )| A. | a>b | B. | a<b | C. | a=b | D. | 不能判断 |
1.丹江口水库是亚洲第一大人工淡水湖,国家南水北调中线工程水源地,总库容达到290.5亿立方米,将290.5亿用科学记数法表示为( )
| A. | 2.905×108 | B. | 2.905×109 | C. | 2.905×1010 | D. | 2.905×1011 |
15. 如图,在三角形纸片ABC中,∠B=∠C=35°,过边BC上的一点,沿与BC垂直的方向将它剪开,分成三角形和四边形两部分,则在四边形中,最大的内角的度数为( )
如图,在三角形纸片ABC中,∠B=∠C=35°,过边BC上的一点,沿与BC垂直的方向将它剪开,分成三角形和四边形两部分,则在四边形中,最大的内角的度数为( )
 如图,在三角形纸片ABC中,∠B=∠C=35°,过边BC上的一点,沿与BC垂直的方向将它剪开,分成三角形和四边形两部分,则在四边形中,最大的内角的度数为( )
如图,在三角形纸片ABC中,∠B=∠C=35°,过边BC上的一点,沿与BC垂直的方向将它剪开,分成三角形和四边形两部分,则在四边形中,最大的内角的度数为( )| A. | 110° | B. | 115° | C. | 120° | D. | 125° |
 如图,在△ABC中,∠ACB=90°,BC=6,DE垂直平分AC交AB于点E,则DE的长为( )
如图,在△ABC中,∠ACB=90°,BC=6,DE垂直平分AC交AB于点E,则DE的长为( ) 如图,在△ABC中,∠C=90°,AB=30,D是AB上一点,AD:CD=25:7,且DB=DA,过AB上一点P,作PE⊥AC于E,PF⊥BD于F,则PE+PF长是18.
如图,在△ABC中,∠C=90°,AB=30,D是AB上一点,AD:CD=25:7,且DB=DA,过AB上一点P,作PE⊥AC于E,PF⊥BD于F,则PE+PF长是18.