题目内容
16. 如图,每个小正方形的边长都是1,
如图,每个小正方形的边长都是1,(1)求四边形ABCD的周长和面积;
(2)∠BCD是直角吗?
分析 (1)利用勾股定理求出AB、BC、CD和DA的长,即可求出四边形ABCD的周长;利用分割法即可求出四边形的面积;
(2)连接BD,求出BD的长,利用勾股定理的逆定理即可证明出结论.
解答  解:(1)AB=$\sqrt{26}$,AD=$\sqrt{17}$,CD=$\sqrt{5}$,BC=2$\sqrt{5}$,
解:(1)AB=$\sqrt{26}$,AD=$\sqrt{17}$,CD=$\sqrt{5}$,BC=2$\sqrt{5}$,
四边形ABCD的周长为$\sqrt{26}+3\sqrt{5}+\sqrt{17}$;
面积为5×5-$\frac{1}{2}$×1×5-$\frac{1}{2}$×1×4-1-$\frac{1}{2}$×1×2-$\frac{1}{2}$×2×4=14.5;
(2)连接BD,
∵BC=2$\sqrt{5}$,CD=$\sqrt{5}$,BD=5,
∴BC2+CD2=BD2,
∴△BCD是直角三角形,
∴∠BCD是直角.
点评 本题主要考查了勾股定理以及勾股定理的逆定理的知识,解题的关键是掌握勾股定理以及逆定理的应用,此题难度不大.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
8.甲,乙,丙,丁四名跳高运动员赛前几次选拔赛成绩如表所示,根据表中的信息,如果要从中,选择一名成绩好又发挥稳定的运动员参加比赛,那么应选甲.
| 甲 | 乙 | 丙 | 丁 | |
| 平均数(cm) | 185 | 180 | 185 | 180 |
| 方差 | 3.6 | 3.6 | 7.9 | 8.2 |
 如图,在△ABC中,∠C=90°,AB=30,D是AB上一点,AD:CD=25:7,且DB=DA,过AB上一点P,作PE⊥AC于E,PF⊥BD于F,则PE+PF长是18.
如图,在△ABC中,∠C=90°,AB=30,D是AB上一点,AD:CD=25:7,且DB=DA,过AB上一点P,作PE⊥AC于E,PF⊥BD于F,则PE+PF长是18.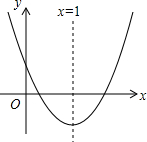 如图,抛物线y=ax2+bx+c(a≠0)与y轴的正半轴相交,顶点在第四象限,对称轴为x=1,下列结论:①b<0;②a+b<0;③$\frac{b}{c}$<-2;④an2+bn=a(2-n)2+b(2-n)(n为任意实数),其中正确的结论个数是( )
如图,抛物线y=ax2+bx+c(a≠0)与y轴的正半轴相交,顶点在第四象限,对称轴为x=1,下列结论:①b<0;②a+b<0;③$\frac{b}{c}$<-2;④an2+bn=a(2-n)2+b(2-n)(n为任意实数),其中正确的结论个数是( ) 如图,AD是△ABC的中线,点E是AD的中点,若△ABC的面积是16,则△BEC的面积是8.
如图,AD是△ABC的中线,点E是AD的中点,若△ABC的面积是16,则△BEC的面积是8.