题目内容
15.已知一元二次方程3x2+4x+m=0有实数根,则m的取值范围是( )| A. | m≤$\frac{4}{3}$ | B. | m≥$\frac{4}{3}$ | C. | m<$\frac{4}{3}$ | D. | m>$\frac{4}{3}$ |
分析 先根据一元二次方程3x2+4x+m=0得出a、b、c的值,再根据方程有实数根列出关于m的不等式,求出m的取值范围即可.
解答 解:由一元二次方程3x2+4x+m=0可知a=3,b=4,c=m,
∵方程有实数根,
∴△=42-4×3m≥0,解得m≤$\frac{4}{3}$.
故选:A.
点评 此题考查了一元二次方程根的情况与判别式△的关系:(1)△>0?方程有两个不相等的实数根;(2)△=0?方程有两个相等的实数根;(3)△<0?方程没有实数根.

练习册系列答案
相关题目
 如图,这是一个由小立方块搭成的几何体的俯视图,小正方形中的数字表示在该位置的小立方块的个数.请你画出它的主视图与左视图.
如图,这是一个由小立方块搭成的几何体的俯视图,小正方形中的数字表示在该位置的小立方块的个数.请你画出它的主视图与左视图.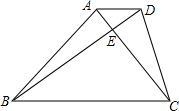 如图,在梯形ABCD中,AD∥BC,对角线AC与BD互相垂直,且BC-AD=4,cos∠DBC=0.8,AC=6.求BC的长及梯形的面积.
如图,在梯形ABCD中,AD∥BC,对角线AC与BD互相垂直,且BC-AD=4,cos∠DBC=0.8,AC=6.求BC的长及梯形的面积.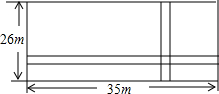 如图,在一块长35m,宽26m的矩形地面上修建同样宽的两条互相垂直的道路(两条道路各与矩形的一条边平行),剩余部分栽种花草,要使剩余部分的面积为850m2,道路的宽应该为多少?
如图,在一块长35m,宽26m的矩形地面上修建同样宽的两条互相垂直的道路(两条道路各与矩形的一条边平行),剩余部分栽种花草,要使剩余部分的面积为850m2,道路的宽应该为多少?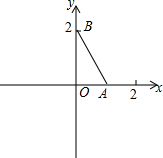 如图,在平面直角坐标系中,已知点A(1,0)和点B(0,2),点C在x轴上,若以A、B、C为顶点构成的三角形是等腰三角形,则满足条件的点C的坐标是(1-$\sqrt{5}$,0),(-1,0),(-$\frac{3}{2}$,0).
如图,在平面直角坐标系中,已知点A(1,0)和点B(0,2),点C在x轴上,若以A、B、C为顶点构成的三角形是等腰三角形,则满足条件的点C的坐标是(1-$\sqrt{5}$,0),(-1,0),(-$\frac{3}{2}$,0).