题目内容
5.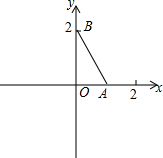 如图,在平面直角坐标系中,已知点A(1,0)和点B(0,2),点C在x轴上,若以A、B、C为顶点构成的三角形是等腰三角形,则满足条件的点C的坐标是(1-$\sqrt{5}$,0),(-1,0),(-$\frac{3}{2}$,0).
如图,在平面直角坐标系中,已知点A(1,0)和点B(0,2),点C在x轴上,若以A、B、C为顶点构成的三角形是等腰三角形,则满足条件的点C的坐标是(1-$\sqrt{5}$,0),(-1,0),(-$\frac{3}{2}$,0).
分析 根据勾股定理求得AB的长,然后分三种情况讨论得到点C的坐标.
解答 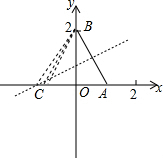 解:∵A(1,0),B(0,2),
解:∵A(1,0),B(0,2),
∴OA=1.OB=2,
∴AB=$\sqrt{5}$,
①当AB=AC时,则OC=$\sqrt{5}$-1,
∴C(1-$\sqrt{5}$,0),
②当AB=BC时,点C在x轴上,且在A的左侧,则OC=OA=1,
∴C(-1,0),
③当AC=BC,则OC2=AC2-OA2,即OC2=(1+OC)2-22,
∴OC=$\frac{3}{2}$,
∴C(-$\frac{3}{2}$,0),
综上所述:C(1-$\sqrt{5}$,0),(-1,0),(-$\frac{3}{2}$,0).
故答案为(1-$\sqrt{5}$,0),(-1,0),(-$\frac{3}{2}$,0).
点评 本题考查了等腰三角形的性质及坐标与图形性质,做题时需注意两点,一是注意点C必须位于坐标轴上,二是注意不能漏解,应分AB为底边和腰两种情况分别解答,难度适中.

练习册系列答案
 举一反三同步巧讲精练系列答案
举一反三同步巧讲精练系列答案 口算与应用题卡系列答案
口算与应用题卡系列答案 名师点睛字词句段篇系列答案
名师点睛字词句段篇系列答案
相关题目
15.已知一元二次方程3x2+4x+m=0有实数根,则m的取值范围是( )
| A. | m≤$\frac{4}{3}$ | B. | m≥$\frac{4}{3}$ | C. | m<$\frac{4}{3}$ | D. | m>$\frac{4}{3}$ |
10.以下画图顺序不正确的是( )
| A. | 直线AB经过点C,画法:先画点C,再画过点C的直线AB | |
| B. | 点C在直线AB上,画法:先画直线AB,再在AB上画一点C | |
| C. | 点G在直线a上但不在直线b上,画法:先画直线a,在a上画一点G,再画不过G的任一条直线b | |
| D. | 直线a与直线b相交于点O,画法:先画直线a或b,再画与直线a或b相交于点O的直线b或a |
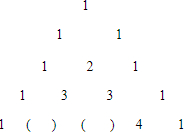 (1)观察下列已有的规律,在括号内填上恰当的数.
(1)观察下列已有的规律,在括号内填上恰当的数.