题目内容
7.在解方程组$\left\{\begin{array}{l}{ax+5y=15}\\{4x-by=-2}\end{array}\right.$时,由于粗心,甲看错了方程组中的a,而得解为$\left\{\begin{array}{l}{x=-3}\\{y=-1}\end{array}\right.$.乙看错了方程组中的b,而得解为$\left\{\begin{array}{l}{x=5}\\{y=4}\end{array}\right.$.(1)甲把a看成了什么,乙把b看成了什么;
(2)求出原方程组的正确解.
分析 (1)将$\left\{\begin{array}{l}{x=-3}\\{y=-1}\end{array}\right.$代入方程组可求得错a和正确的b,将$\left\{\begin{array}{l}{x=5}\\{y=4}\end{array}\right.$代入方程组可求得错b和正确的a;
(2)然后将正确的a、b的值代入求解即可.
解答 解:(1)将$\left\{\begin{array}{l}{x=-3}\\{y=-1}\end{array}\right.$代入原方程组得$\left\{\begin{array}{l}{-3a-5=15}\\{4×(-3)+b=-2}\end{array}\right.$解得$\left\{\begin{array}{l}{{a}_{错}=-\frac{20}{3}}\\{b=10}\end{array}\right.$.
将$\left\{\begin{array}{l}{x=5}\\{y=4}\end{array}\right.$代入原方程组得$\left\{\begin{array}{l}{5a+20=15}\\{20-4b=-2}\end{array}\right.$,解得$\left\{\begin{array}{l}{a=-1}\\{{b}_{错}=\frac{11}{2}}\end{array}\right.$,
∴甲把a看成-$\frac{20}{3}$,乙把b看成了$\frac{11}{2}$.
(2)由(1)可知原方程组中a=-1,b=10.故原方程组为$\left\{\begin{array}{l}{-x+5y=15}\\{4x-10y=-2}\end{array}\right.$,解得$\left\{\begin{array}{l}{x=14}\\{y=\frac{29}{5}}\end{array}\right.$.
点评 本题主要考查的是解二元一次方程组、二元一次方程组的解,掌握二元一次方程组的解法是解题的关键.

 小学课时特训系列答案
小学课时特训系列答案| A. | 7cm | B. | 17cm | C. | 12cm | D. | 7cm或17cm |
| A. | (-2,3) | B. | (-3,2) | C. | (3,-2) | D. | (3,2) |
 如图,把长方形ABCD沿EF对折后,使四边形ABFE与四边形HGFE重合,若∠1=50°,则∠AEF的度数为( )
如图,把长方形ABCD沿EF对折后,使四边形ABFE与四边形HGFE重合,若∠1=50°,则∠AEF的度数为( )| A. | 110° | B. | 115° | C. | 120° | D. | 130° |
九(一)班:168 167 170 165 168 166 171 168 167 170
九(二)班:165 167 169 170 165 168 170 171 168 167
(1)补充完成下面的统计分析表:
| 班级 | 平均数 | 方差 | 中位数 |
| 一班 | 168 | 3.2 | 168 |
| 二班 | 168 | 3.8 | 168 |
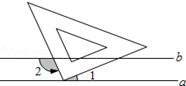 如图,小华把三角板的直角顶点放在直线a上,两条直角边与直线b相交,如果a∥b,且∠1=40°,则∠2的度数为( )
如图,小华把三角板的直角顶点放在直线a上,两条直角边与直线b相交,如果a∥b,且∠1=40°,则∠2的度数为( )| A. | 100° | B. | 110° | C. | 120° | D. | 130° |
 如图,如果AC∥BD,CE∥DF,那么△ACE与△BDF是否相似?△ACE与△BDF是否位似?试说明理由.
如图,如果AC∥BD,CE∥DF,那么△ACE与△BDF是否相似?△ACE与△BDF是否位似?试说明理由.