题目内容
16. 如图,矩形ABCD中,AB=20,BC=10,若在AB、AC上各取一点N、M,使得BM+MN的值最小,这个最小值为16.
如图,矩形ABCD中,AB=20,BC=10,若在AB、AC上各取一点N、M,使得BM+MN的值最小,这个最小值为16.
分析 过B点作AC的垂线,使AC两边的线段相等,到E点,过E作EF垂直AB交AB于F点,EF就是所求的线段.
解答  解:过B点作AC的垂线,垂足为Q,延长BQ到E,使BQ=QE,过E作EF垂直AB交AB于F点,
解:过B点作AC的垂线,垂足为Q,延长BQ到E,使BQ=QE,过E作EF垂直AB交AB于F点,
AC=$\sqrt{A{B}^{2}+B{C}^{2}}$=10$\sqrt{5}$,
∵S△ABC=$\frac{1}{2}$AC•BQ=$\frac{1}{2}$AB•BC,
∴AC边上的高BQ=$\frac{20×10}{10\sqrt{5}}$=4$\sqrt{5}$,
BE=2BQ=8$\sqrt{5}$.
∵∠ABQ=∠EBF,∠AQB=∠EFB=90°,
∴△BEF∽△BAQ,
∵△BAQ∽△CAB
∵△CAB∽△BEF,
∴$\frac{AB}{EF}$=$\frac{AC}{BE}$,即$\frac{20}{EF}$=$\frac{10\sqrt{5}}{8\sqrt{5}}$
EF=16.
故答案为16.
点评 本题考查最短路径问题,关键确定何时路径最短,然后运用勾股定理和相似三角形的性质求得解.

练习册系列答案
相关题目
1.下列命题,正确的是( )
| A. | 平分弦的直径垂直于弦 | |
| B. | 正多边形是中心对称图形 | |
| C. | 四个角是直角的四边形是正方形 | |
| D. | 三角形的一条中线能将其分成面积相等的两部分 |
6.如图所示四个图形中,不是轴对称图形的是( )
| A. |  | B. |  | C. |  | D. |  |
 .
. 
 如图,在矩形纸片ABCD中,AB<BC.点M、N分别在边AD、BC上,沿直线MN将四边形DMNC翻折,点C恰好与点A重合.如果此时在原图中△CDM与△MNC的面积比是1:3,那么$\frac{MN}{DM}$的值等于$2\sqrt{3}$.
如图,在矩形纸片ABCD中,AB<BC.点M、N分别在边AD、BC上,沿直线MN将四边形DMNC翻折,点C恰好与点A重合.如果此时在原图中△CDM与△MNC的面积比是1:3,那么$\frac{MN}{DM}$的值等于$2\sqrt{3}$.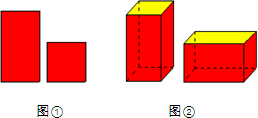 如图①的长方形和正方形纸板做侧面和底面,做成如图②的竖式和横式的两种无盖纸盒,现在仓库里有100张正方形纸板和250张长方形纸板,如果做这两种纸盒若干个,恰好使库存的纸板用完,则竖式和横式纸盒一共可做70个.
如图①的长方形和正方形纸板做侧面和底面,做成如图②的竖式和横式的两种无盖纸盒,现在仓库里有100张正方形纸板和250张长方形纸板,如果做这两种纸盒若干个,恰好使库存的纸板用完,则竖式和横式纸盒一共可做70个.