题目内容
8. 如图,在矩形纸片ABCD中,AB<BC.点M、N分别在边AD、BC上,沿直线MN将四边形DMNC翻折,点C恰好与点A重合.如果此时在原图中△CDM与△MNC的面积比是1:3,那么$\frac{MN}{DM}$的值等于$2\sqrt{3}$.
如图,在矩形纸片ABCD中,AB<BC.点M、N分别在边AD、BC上,沿直线MN将四边形DMNC翻折,点C恰好与点A重合.如果此时在原图中△CDM与△MNC的面积比是1:3,那么$\frac{MN}{DM}$的值等于$2\sqrt{3}$.
分析 由折叠的性质可得:∠AMN=∠CMN,由四边形ABCD是矩形,可得∠AMN=∠CNM,则可证得∠CNM=∠CMN,继而可得CM=CN;过点M作MH⊥BC于点H,由△CDM的面积与△MNC的面积比为1:3,易得NC=3MD=3HC,然后设DM=x,由勾股定理,可求得MN的长,继而求得答案.
解答 解:由折叠的性质可得:∠EMN=∠DMN,
即∠EMN=∠EMA+∠AMN,
∠DMN=∠DMC+∠CMN,
∵∠EMA=∠DMC
∴∠AMN=∠CMN,
∵四边形ABCD是矩形,
∴AD∥BC,
∴∠AMN=∠CNM,
∴∠CNM=∠CMN,
∴CM=CN,
如图,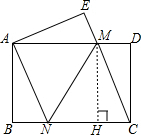
过点M作MH⊥BC于点H,则四边形MHCD是矩形,
∴HC=DM,MH=DC,
∵△CDM的面积与△CMN的面积比为1:3,
∴$\frac{{S}_{△CDM}}{{S}_{△CMN}}$=$\frac{\frac{1}{2}DM•MH}{\frac{1}{2}CN•NH}=\frac{DM}{CN}=\frac{1}{3}$,
∴NC=3MD=3HC,
∴NH=2HC,
设DM=x,则HC=x,NH=2x,
∴CM=CN=3x,
在Rt△CDM中,DC=$\sqrt{C{M}^{2}-D{M}^{2}}$=2$\sqrt{2}$x,
∴HM=2$\sqrt{2}$x,
在Rt△MNH中,MN=$\sqrt{M{H}^{2}+N{H}^{2}}$=2$\sqrt{3}$x,
∴$\frac{MN}{DM}=\frac{2\sqrt{3}x}{x}$=2$\sqrt{3}$.
故答案为:2$\sqrt{3}$.
点评 此题考查了矩形的性质、折叠的性质、勾股定理以及三角形的面积.此题难度适中,注意掌握辅助线的作法,注意掌握数形结合思想与方程思想的应用.

| A. | (1,1) | B. | (-1,-1) | C. | (1,-1) | D. | (-1,1) |
| A. | (a+b)2=a2+b2 | B. | (-2a)3=-6a3 | C. | (a2b)3=a5b2 | D. | (-a)6÷(-a)2=a4 |
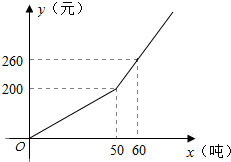 已知某市2014年企业用水量x(吨)与该月应交的水费y(元)之间的函数关系如图.
已知某市2014年企业用水量x(吨)与该月应交的水费y(元)之间的函数关系如图. 如图,矩形ABCD中,AB=20,BC=10,若在AB、AC上各取一点N、M,使得BM+MN的值最小,这个最小值为16.
如图,矩形ABCD中,AB=20,BC=10,若在AB、AC上各取一点N、M,使得BM+MN的值最小,这个最小值为16.