题目内容
13.某工厂生产的一种产品按质量分为10个档次,若生产第一档次(最低档)的产品,则一天可以生产76件,每件的利润为10元.每提高一个档次,每件的利润增加2元,每天的产量将减少4件.设生产的产品质量的档次(每天只生产一个档次的产品)为x时,一天的利润为y元.(1)用含x的代数式分别表示出每件产品的利润及每天生产的件数.
(2)若生产该产品一天的总利润为1080元,则该工厂生产的是第几档次的产品?
分析 (1)每件的利润为10+2(x-1),生产件数为76-4(x-1),则y=[10+2(x-1)][76-4(x-1)];
(2)由题意可令y=1080,求出x的实际值即可;
解答 解(1)据题意可得y=[10+2(x-1)][76-4(x-1)],
整理,得y=-8x2+128x+640;
(2)当利润是1080元时,即-8x2+128x+640=1080
解得x1=5,x2=11,
因为x=11>10,不符合题意,舍去.
因此取x=5,
当生产产品的质量档次是在第5档次时,一天的总利润为1080元.
点评 此题考查的是二次函数的实际应用和一元二次方程的应用,难度一般,注意,在市场营销问题中,一件的利润和件数,一个量增加的同时,另一个量会减少,要根据题意,正确使用,先确定二次函数,再解一元二次方程,由一般到特殊.

练习册系列答案
 名校练考卷期末冲刺卷系列答案
名校练考卷期末冲刺卷系列答案
相关题目
3.小张为自己已经用光话费的手机充值100元,他购买的服务是:20元/月包接听,主叫0.2元/分钟.这个月内,他手机所存话费y(元)与主叫时间t(分钟)之间的函数关系是( )
| A. | y=100-0.2t | B. | y=80-0.2t | C. | y=100+0.2t | D. | y=80+0.2t |
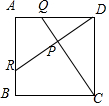 图中ABCD为正方形,Q及R分别为AD及AB上的点,DR与CQ相交于P,已知AQ=BR.
图中ABCD为正方形,Q及R分别为AD及AB上的点,DR与CQ相交于P,已知AQ=BR.