题目内容
2.如图①,在△ABC中,AB=BC=6cm,O为AC边上一点,且OA=OB=OC,点D射线AB上一点,连接OD,过点O作OE⊥OD,交射线BC于点E.(1)若点D在线段AB上,OD与OE相等吗?请说明理由.
(2)四边形ODBE的面积是否发生变化?若变化,请说明理由;若不变化,请求出四边形ODBE的面积.
(3)AD=3时,△AOD≌△COE.
(4)如图②,若点D在线段AB的延长线,OD与OE相等吗?请说明理由.

分析 (1)结论OD=OE.只要证明△OBD≌△OCE即可;
(2)由△OBD≌△OCE,推出S△OBD=S△OCE,推出S四边形ODBE=S△OBC=$\frac{1}{2}$S△ABC即可解决问题;
(3)当AD=3时,易证AD=BD=BE=CE,△AOD≌△COE;
(4)结论:OD=OE.只要证明△OBD≌△OCE即可;
解答 解:(1)如图①中,结论:OD=OE.理由如下: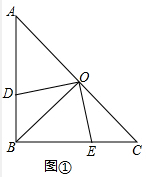
∵OA=OB=OC,
∴△ABC是直角三角形,
∴∠ABC=90°,
∵BA=BC,∠C=∠A=∠ABO=45°,OA=OC,
∴BO⊥AC,∵OE⊥OD,
∴∠BOC=∠DOE=90°,
∴∠DOB=∠EOC,
∵OB=OC,∠OBD=∠C,
∴△OBD≌△OCE,
∴OD=OE.
(2)四边形ODBE的面积不变.
理由:∵△OBD≌△OCE,
∴S△OBD=S△OCE,
∴S四边形ODBE=S△OBC=$\frac{1}{2}$S△ABC=$\frac{1}{2}$×$\frac{1}{2}$×6×6=9(cm2),
∴四边形ODBE的面积不变.
(3)当AD=3时,易证AD=BD=BE=CE,△AOD≌△COE.
故答案为3.
(4)如图2中,结论:OD=OE.理由如下: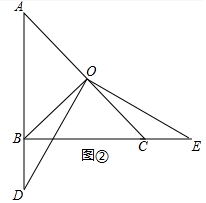
∵OA=OB=OC,
∴△ABC是直角三角形,
∴∠ABC=90°,
∵BA=BC,∠ACB=∠A=∠ABO=45°,OA=OC,
∴BO⊥AC,∵OE⊥OD,
∴∠BOC=∠DOE=90°,
∴∠DOB=∠EOC,
∵OB=OC,∠OBD=∠OCE=135°,
∴△OBD≌△OCE,
∴OD=OE.
点评 本题考查四边形综合题、等腰直角三角形的判定和性质、全等三角形的判定和性质、四边形面积问题等知识,解题的关键是正确寻找全等三角形解决问题,属于中考常考题型.

练习册系列答案
 小学教材全测系列答案
小学教材全测系列答案 小学数学口算题卡脱口而出系列答案
小学数学口算题卡脱口而出系列答案 优秀生应用题卡口算天天练系列答案
优秀生应用题卡口算天天练系列答案 浙江之星课时优化作业系列答案
浙江之星课时优化作业系列答案
相关题目
10.学校准备推荐一位老师参加业务技能比赛,对甲、乙两位老师进行三项测试,他们各自的成绩(百分制)如下表:
学校将课件制作、片段教学、综合素质按三项得分的2:3:5确定最终成绩,并根据成绩择优推荐,请你通过计算说明谁被推荐参加比赛?
| 选手 | 课件制作 | 片段教学 | 综合素质 |
| 甲 | 85 | 78 | 85 |
| 乙 | 73 | 80 | 82 |
 如图,△ABC中,AD=BD,AE=EC,BC=6,则DE=3.
如图,△ABC中,AD=BD,AE=EC,BC=6,则DE=3.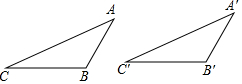 如图,∠B=∠B′>90°,AB=A′B′,AC=A′C′.求证:△ABC≌△A′B′C′.
如图,∠B=∠B′>90°,AB=A′B′,AC=A′C′.求证:△ABC≌△A′B′C′.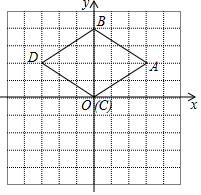 如图所示,△DBC是由△ABC经过变换得到的图形,分别写出点A、B、C、D的坐标,观察点A与点D的坐标之间的关系,如果△ABC中任一点N的坐标为N(x,y),它在△BCD中的对应点M的坐标是什么?
如图所示,△DBC是由△ABC经过变换得到的图形,分别写出点A、B、C、D的坐标,观察点A与点D的坐标之间的关系,如果△ABC中任一点N的坐标为N(x,y),它在△BCD中的对应点M的坐标是什么? 如图网格中每个小正方形的边长为1,阴影部分是一条可爱的小鱼,若把这条鱼剪拼成一个正方形,那么新正方形的边长是$\sqrt{6}$.
如图网格中每个小正方形的边长为1,阴影部分是一条可爱的小鱼,若把这条鱼剪拼成一个正方形,那么新正方形的边长是$\sqrt{6}$.