题目内容
17．
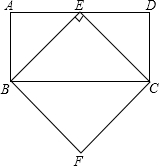如图，在矩形ABCD中，AD=2CD，E是AD的中点，BF∥CE，CF∥BE．求证：四边形BECF是正方形．
分析 利用全等三角形的判定与性质结合平行四边形以及正方形的判定方法得出即可．
解答 证明：∵BF∥CE，CF∥BE，
∴四边形EBFC是平行四边形，
∵在矩形ABCD中，AD=2CD，E是AD的中点，
∴AE=AB=DE=DC，
在△ABE和△CDE中，
∵$\left\{\begin{array}{l}{AB=DC}\\{∠A=∠D}\\{AE=DE}\end{array}\right.$，
∴△ABE≌△CDE（SAS），
∴BE=EC，∠AEB=∠DEC=45°，
∴∠BEC=90°，
∴四边形EBFC是正方形．
点评 此题主要考查了全等三角形的判定与性质以及正方形的判定，得出△ABE≌△CDE是解题关键．
练习册系列答案
综合自测系列答案
相关题目
等边三角形ABC的边长为6，点E在AC边上从点A向点C运动，同时点F在BC边上从点C向点B运动，速度相同，连接AF，BE相交于点P．当点E从点A运动到点C时，则点P经过的路径长$\frac{4\sqrt{3}}{3}$π．
如图，Rt△ABC中，BD是斜边AC上的高线，E，F分别是AC，AB上的点，若∠1=∠2，则EF∥BD．试说明理由．