题目内容
7. 如图,Rt△ABC中,BD是斜边AC上的高线,E,F分别是AC,AB上的点,若∠1=∠2,则EF∥BD.试说明理由.
如图,Rt△ABC中,BD是斜边AC上的高线,E,F分别是AC,AB上的点,若∠1=∠2,则EF∥BD.试说明理由.
分析 在Rt△ABC中,由直角三角形的两锐角互余,可得∠1+∠A=90°,然后由∠1=∠2,可得∠2+∠A=90°,然后由BD⊥AC,可得∠ADB=90°,然后根据同位角相等,两直线平行,即可得到EF∥BD.
解答 解:在Rt△ABC中,
∵∠1+∠A=90°,∠1=∠2,
∴∠2+∠A=90°,
∵∠2+∠A+∠AEF=180°,
∴∠AEF=90°,
∵BD是斜边AC上的高线,
∴∠ADB=90°,
∴∠AEF=∠ADB,
∴EF∥BD.
点评 本题主要考查平行线的判定,掌握平行线的性质和判定是解题的关键,即①两直线平行?同位角相等,②两直线平行?内错角相等,③两直线平行?同旁内角互补,④a∥b,b∥c⇒a∥c

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
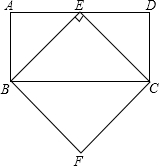 如图,在矩形ABCD中,AD=2CD,E是AD的中点,BF∥CE,CF∥BE.求证:四边形BECF是正方形.
如图,在矩形ABCD中,AD=2CD,E是AD的中点,BF∥CE,CF∥BE.求证:四边形BECF是正方形. 如图,∠1=∠3,∠2=120°,求∠4的度数.
如图,∠1=∠3,∠2=120°,求∠4的度数.