Question

如图，直线y₁=﹣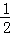x+2与x轴，y轴分别交于B，C，抛物线y=ax²+bx+c（a≠0）经过点A，B，C，点A坐标为（﹣1，0）．

（1）求抛物线的解析式；

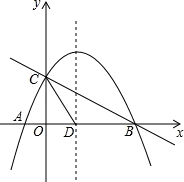
（2）抛物线的对称轴与x轴交于点D，连接CD，点P是直线BC上方抛物线上的一动点（不与B，C重合），当点P运动到何处时，四边形PCDB的面积最大？求出此时四边形PCDB面积的最大值和点P坐标；

（3）在抛物线上的对称轴上是否存在一点Q，使△QCD是以CD为腰的等腰三角形？若存在，直接写出点Q的坐标；若不存在，请说明理由．

Answer 1

【考点】二次函数综合题．

【分析】（1）分别令解析式y=﹣x+2中x=0和y=0，求出点B、点C的坐标；设二次函数的解析式为y=ax²+bx+c，将点A、B、C的坐标代入解析式，求出a、b、c的值，进而求得解析式；

（2）设出M点的坐标为（a，﹣a+2），就可以表示出P的坐标，由四边形PCDB的面积=S_△BCD+S_△CPM+S_△PMB求出S与a的关系式，由二次函数的性质就可以求出结论；

（3）由（2）的解析式求出顶点坐标，再由勾股定理求出CD的值，再以点C为圆心，CD为半径作弧交对称轴于Q₁，以点D为圆心CD为半径作圆交对称轴于点Q₂，Q₃，作CE垂直于对称轴与点E，由等腰三角形的性质及勾股定理就可以求出结论．

【解答】解：（1）令x=0，可得y=2，

令y=0，可得x=4，

即点B（4，0），C（0，2）；

设二次函数的解析式为y=ax²+bx+c，

将点A、B、C的坐标代入解析式得，

，

解得：，

即该二次函数的关系式为y=﹣x²+x+2；

（2）如图1，过点P作PN⊥x轴于点N，交BC于点M，过点C作CE⊥PN于E，

设M（a，﹣a+2），P（a，﹣a²+a+2），

∴PM=﹣a²+a+2﹣（﹣a+2）=﹣a²+2a（0≤x≤4）．

∵y=﹣x²+x+2=﹣（x﹣）²+，

∴点D的坐标为：（，0），

∵S_{四边形PCDB}=S_△BCD+S_△CPM+S_△PMB=BD•OC+PM•CE+PM•BN，

=+a（﹣a²+2a）+（4﹣a）（﹣a²+2a），

=﹣a²+4a+（0≤x≤4）．

=﹣（a﹣2）²+

∴a=2时，S_{四边形PCDB的面积最大}=，

∴﹣a²+a+2=﹣×2²+×2+2=3，

∴点P坐标为：（2，3），

∴当点P运动到（2，3）时，四边形PCDB的面积最大，最大值为；

（3）如图2，∵抛物线的对称轴是x=．

∴OD=．

∵C（0，2），

∴OC=2．

在Rt△OCD中，由勾股定理，得

CD=．

∵△CDQ是以CD为腰的等腰三角形，

∴CQ₁=DQ₂=DQ₃=CD．

如图2所示，作CE⊥对称轴于E，

∴EQ₁=ED=2，

∴DQ₁=4．

∴Q₁（，4），Q₂（，），Q₃（，﹣）．

【点评】本题考查了二次函数的综合运用，涉及了待定系数法求二次函数的解析式的运用，勾股定理的运用，等腰三角形的性质的运用，四边形的面积的运用，解答时求出函数的解析式是关键．