题目内容
已知:如图,正方形ABCD的边长为1,点E,F,G,H分别在AB,BC,CD,DA上,且四边形EFGH也是正方形,设AE=x,正方形EFGH的面积为S.
(1)求证:△AEH≌△BFE;
(2)求S与x之间的函数关系式.
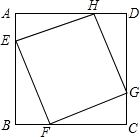
【考点】全等三角形的判定与性质;根据实际问题列二次函数关系式;正方形的性质.
【分析】(1)利用正方形的性质,用AAS证明△AEH≌△BFE;
(2)利用△AEH≌△BFE,得到BF=AE=x,利用勾股定理,在Rt△BFE中,EF2=BF2+BE2=x2+(1﹣x)2,所以S=EF2=x2+(1﹣x)2=2x2﹣2x+1.
【解答】解:(1)∵四边形ABCD为正方形,四边形EFGH也是正方形,
∴∠A=∠B=∠HEF=90°,EH=FE,
∴∠AEH+∠AHE=90°,∠AEH+∠BEF=90°,
∴∠AHE=∠BEF,
在△AEH和△BFE中,
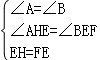 ,
,
∴△AEH≌△BFE.
(2)∵△AEH≌△BFE,
∴BF=AE=x,(0<x<1)
在Rt△BFE中,EF2=BF2+BE2=x2+(1﹣x)2,
∴S=EF2=x2+ (1﹣x)2=2x2﹣2x+1,(0<x<1)
(1﹣x)2=2x2﹣2x+1,(0<x<1)
【点评】本题考查了正方形的性质、全等三角形的性质与判定,解决本题的关键是证明)△AEH≌△BFE.

练习册系列答案
 智趣寒假作业云南科技出版社系列答案
智趣寒假作业云南科技出版社系列答案
相关题目
 C.﹣
C.﹣
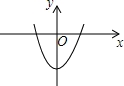
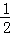 x+2与x轴,y轴分别交于B,C,抛物线y=ax2+bx+c(a≠0)经过点A,B,C,点A坐标为(﹣1,0).
x+2与x轴,y轴分别交于B,C,抛物线y=ax2+bx+c(a≠0)经过点A,B,C,点A坐标为(﹣1,0).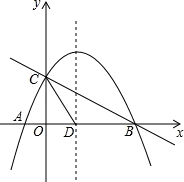
 =0的根的情况为( )
=0的根的情况为( ) 有两个相等的实数根,求m的值,并求出方程的解.
有两个相等的实数根,求m的值,并求出方程的解.