题目内容
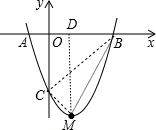
抛物线y=ax2+bx+c(a≠0)与x轴交于点A(﹣1,0),B(3,0)两点,与y轴交于点C(0,﹣3).
(1)求该抛物线的解析式及顶点M的坐标;
(2)当y的值大于0时,求x的取值范围;
(3)分别求出△BCM与△ABC的面积.

【考点】抛物线与x轴的交点.
【专题】计算题.
【分析】(1)由于已知抛物线与x轴的交点坐标,则可设交点式y=a(x+1)(x﹣3),然后把(0,﹣3)代入求出a即可得到抛物线解析式,再配成顶点式得到M点坐标;
(2)观察函数图象,写出抛物线在x轴上方部分所对应的自变量的范围即可;
(3)根据三角形面积公式计算△ABC的面积,利用S△BCM=S梯形OCMD+S△BMD﹣S△BOC计算△BCM的面积.
【解答】解:(1)设抛物线解析式为y=a(x+1)(x﹣3),
∵抛物线过点(0,﹣3),
∴﹣3=a(0+1)(0﹣3),
∴a=1,
∴抛物线解析式为y=(x+1)(x﹣3),即y=x2﹣2x﹣3,
∵y=x2﹣2x﹣3=(x﹣1)2﹣4,
∴顶点M(1,﹣4);
(2)x<﹣1或x>3;
(3)如图,连接BC、BM、CM,作MD⊥x轴于D,
S△BCM=S梯形OCMD+S△BMD﹣S△BOC=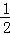 ×(3+4)×1+
×(3+4)×1+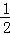 ×2×4﹣
×2×4﹣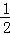 ×3×3=3
×3×3=3
S△ABC=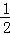 ×4×3=6.
×4×3=6.
【点评】本题考查了抛物线与x轴的交点:从二次函数的交点式y=a(x﹣x1)(x﹣x2)(a,b,c是常数,a≠0)可直接得到抛物线与x轴的交点坐标(x1,0),(x2,0).也考查了待定系数法求抛物线解析式和三角形面积公式.

练习册系列答案
相关题目
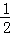 x+2与x轴,y轴分别交于B,C,抛物线y=ax2+bx+c(a≠0)经过点A,B,C,点A坐标为(﹣1,0).
x+2与x轴,y轴分别交于B,C,抛物线y=ax2+bx+c(a≠0)经过点A,B,C,点A坐标为(﹣1,0).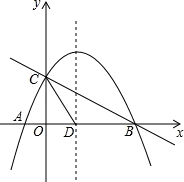
 有两个相等的实数根,求m的值,并求出方程的解.
有两个相等的实数根,求m的值,并求出方程的解.

 是( )
是( )