题目内容
10．
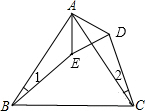如图，点E是等边△ABC内一点，∠1=∠2，BE=CD，则△ADE的形状是（ ）| A． | 底边和腰不相等的等腰三角形 | B． | 等边三角形 | ||
| C． | 直角三角形 | D． | 等腰直角三角形 |
分析 先证得△ABE≌△ACD，可得AE=AD，∠BAE=∠CAD=60°，即可证明△ADE是等边三角形．
解答 解：∵△ABC为等边三角形，
∴AB=AC，
在△ABE≌△ACD中，
$\left\{\begin{array}{l}{AB=AC}\\{∠1=∠2}\\{BE=CD}\end{array}\right.$，
∴△ABE≌△ACD，
∴AE=AD，∠BAE=∠CAD=60°，
∴△ADE是等边三角形．
故选B．
点评 此题主要考查学生对等边三角形的判定及三角形的全等等知识点，熟练掌握全等三角形的判定与性质是解决问题的关键．
练习册系列答案
亮点激活精编提优100分大试卷系列答案
相关题目
如图，AB为⊙O的直径，弦CD⊥AB于F，∠CAB=36°，求∠D的度数．
用三角尺画角平分线：如图，∠AOB是一个任意角，在边OA，OB上分别取OM=ON，再分别用三角尺过M、N作OA，OB的垂线，交点为P，画射线OP，则这条射线即为∠AOB的平分线．请解释这种画角平分线方法的道理．
18．
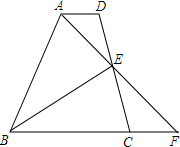在梯形ABCD中，AD∥BC，E为CD的中点，BE⊥AE，AE的延长线交BC的延长线于点F．
（1）求证：AE是∠BAD的平分线；
（2）当∠D=90°，∠ABC=60°，AB=12时，求AD的长．
在梯形ABCD中，AD∥BC，E为CD的中点，BE⊥AE，AE的延长线交BC的延长线于点F．（1）求证：AE是∠BAD的平分线；
（2）当∠D=90°，∠ABC=60°，AB=12时，求AD的长．
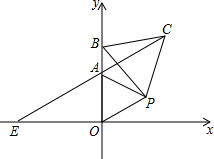如图，在平面直角坐标系中，△AOP为等边三角形，A点坐标为（0，1），点B为y轴上位于A点上方的一个动点，以BP为边向BP的右侧作等边△PBC，连接CA，并延长CA交x轴于点E．
已知：如图，O是AB的中点，DC∥AB．求证：AE=CF．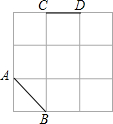
操作题：如图，在3×3网格中，已知线段AB、CD，以格点为端点画一条线段，使它与AB、CD组成轴对称图形．（画出所有可能）