题目内容
14.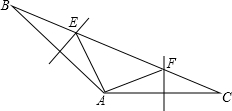 已知△ABC中,∠BAC=140°,BC=12,AB、AC的垂直平分线分别交BC于E、F,求∠EAF的度数和△AEF的周长.
已知△ABC中,∠BAC=140°,BC=12,AB、AC的垂直平分线分别交BC于E、F,求∠EAF的度数和△AEF的周长.
分析 由AB、AC的垂直平分线分别交BC于E、F,可得AE=BE,AF=CF,继而可得△AEF的周长=BC,∠BAE+∠CAF=∠B+∠C,继而求得答案.
解答 解:∵AB、AC的垂直平分线分别交BC于E、F,
∴AE=BE,AF=CF,
∴△AEF的周长=AE+AF+EF=BE+EF+CF=BC=12;
∵△ABC中,∠BAC=140°,
∴∠B+∠C=180°-∠BAC=40°,
∵AE=BE,AF=CF,
∴∠BAE=∠B,∠CAF=∠C,
∴∠BAE+∠CAF=∠B+∠C=40°,
∴∠EAF=∠BAC-(∠BAE+∠CAF)=100°.
点评 此题考查了线段垂直平分线的性质.注意求得∠BAE+∠CAF=∠B+∠C是关键.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
19.若2x2+1与1互为相反数,则x为( )
| A. | 1或0 | B. | 0 | C. | -1或0 | D. | 无解 |
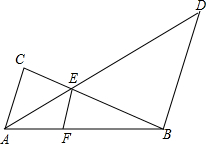 如图,AC∥BD,AD和BC相交于点E,EF∥AC交AB于点F,且AE=p,BD=q,EF=r.
如图,AC∥BD,AD和BC相交于点E,EF∥AC交AB于点F,且AE=p,BD=q,EF=r.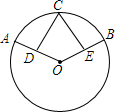 如图,$\widehat{AC}$=$\widehat{BC}$,D、E分别是半径OA和OB的中点,试判断CD与CE的大小关系,并说明理由.
如图,$\widehat{AC}$=$\widehat{BC}$,D、E分别是半径OA和OB的中点,试判断CD与CE的大小关系,并说明理由.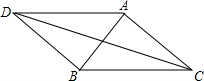 等腰Rt△ABC中,AB=AC,∠BAC=90°,点D在△ABC外,且∠ADB=45°,BD=3,AD=4,求线段DC的长.
等腰Rt△ABC中,AB=AC,∠BAC=90°,点D在△ABC外,且∠ADB=45°,BD=3,AD=4,求线段DC的长.