题目内容
4.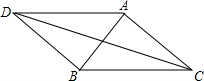 等腰Rt△ABC中,AB=AC,∠BAC=90°,点D在△ABC外,且∠ADB=45°,BD=3,AD=4,求线段DC的长.
等腰Rt△ABC中,AB=AC,∠BAC=90°,点D在△ABC外,且∠ADB=45°,BD=3,AD=4,求线段DC的长.
分析 过B作BE⊥AD于E,过C作CF⊥AD交DA的延长线于F,如图,先证明△ABE≌△AFC得到AE=CF,BE=AF,在Rt△BDE中利用等腰直角三角形的性质得DE=BE=$\frac{\sqrt{2}}{2}$BD=$\frac{3\sqrt{2}}{2}$,则AE=AD-DE=4-$\frac{3\sqrt{2}}{2}$,AF=BE=$\frac{3\sqrt{2}}{2}$,CF=4-$\frac{3\sqrt{2}}{2}$,然后在Rt△CDF中,利用勾股定理计算CD的长.
解答 解:过B作BE⊥AD于E,过C作CF⊥AD交DA的延长线于F,如图,
∵∠BAC=90°,AB=AC,
∴∠1+∠2=90°,∠2+∠3=90°,
∴∠1=∠3,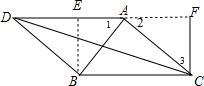
在△ABE与△CAF中,
$\left\{\begin{array}{l}{∠BEA=∠AFC}\\{∠1=∠3}\\{AB=CA}\end{array}\right.$,
∴△ABE≌△AFC,
∴AE=CF,BE=AF,
在Rt△BDE中,∵∠ADB=45°,
∴DE=BE=$\frac{\sqrt{2}}{2}$BD=$\frac{3\sqrt{2}}{2}$,
∴AE=AD-DE=4-$\frac{3\sqrt{2}}{2}$,
∴AF=BE=$\frac{3\sqrt{2}}{2}$,CF=4-$\frac{3\sqrt{2}}{2}$,
在Rt△CDF中,CD=$\sqrt{C{F}^{2}+D{F}^{2}}$=$\sqrt{(4-\frac{3\sqrt{2}}{2})^{2}+(4+\frac{3\sqrt{2}}{2})^{2}}$=$\sqrt{41}$.
点评 本题考查了旋转的性质:对应点到旋转中心的距离相等;对应点与旋转中心所连线段的夹角等于旋转角;旋转前、后的图形全等.也考查了全等三角形的判定与性质、勾股定理和等腰直角三角形的性质.

| A. | 三点确定一个圆 | |
| B. | 正多边形既是轴对称图形也是中心对称图形 | |
| C. | 等弧所对的圆周角相等 | |
| D. | 三角形的外心到三边的距离相等 |
 如图,∠AOB的平分线上一点P到OA的距离为10,Q是OB上任一点,则( )
如图,∠AOB的平分线上一点P到OA的距离为10,Q是OB上任一点,则( )| A. | PQ>10 | B. | PQ≥10 | C. | PQ<10 | D. | PQ≤10 |
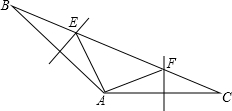 已知△ABC中,∠BAC=140°,BC=12,AB、AC的垂直平分线分别交BC于E、F,求∠EAF的度数和△AEF的周长.
已知△ABC中,∠BAC=140°,BC=12,AB、AC的垂直平分线分别交BC于E、F,求∠EAF的度数和△AEF的周长. 如图,△ABD≌△ACE,点B和点C是对应顶点,AB=9cm,BD=7cm,AD=4cm,则DC=5cm.
如图,△ABD≌△ACE,点B和点C是对应顶点,AB=9cm,BD=7cm,AD=4cm,则DC=5cm. 在△ABC中,BC的垂直平分线,交∠BAC的外角平分线于点D,求证:∠DBA=∠DCA.
在△ABC中,BC的垂直平分线,交∠BAC的外角平分线于点D,求证:∠DBA=∠DCA.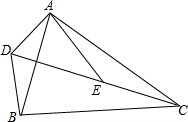 已知$\frac{AD}{AB}=\frac{DE}{BC}=\frac{AE}{AC}$,求证:△ADB∽△AEC.
已知$\frac{AD}{AB}=\frac{DE}{BC}=\frac{AE}{AC}$,求证:△ADB∽△AEC.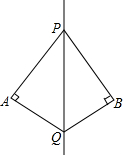 如图,PQ是∠APB的平分线,QA⊥PA于点A,QB⊥PB于点B,试判断点A,B是否关于PQ成轴对称,并说明理由.
如图,PQ是∠APB的平分线,QA⊥PA于点A,QB⊥PB于点B,试判断点A,B是否关于PQ成轴对称,并说明理由.