已知方程x2+5x+m=0有两个相等实数根.则m= ．题目和参考答案——青夏教育精英家教网—

题目内容

已知方程x²+5x+m=0有两个相等实数根，则m=

．

考点：根的判别式

专题：计算题

分析：根据判别式的意义得到△=5²-4×1×m=0，然后解一次方程即．

解答：解：根据得题意△=5²-4×1×m=0，
解得m=

．
故答案为

．

点评：本题考查了根的判别式：一元二次方程ax²+bx+c=0（a≠0）的根与△=b²-4ac有如下关系：当△＞0时，方程有两个不相等的两个实数根；当△=0时，方程有两个相等的两个实数根；当△＜0时，方程无实数根．

练习册系列答案

相关题目

若方程x²-8x+m=0两实数根的平方差为16，则m的值等于（　　）

某出版社对其发行的杂志的质量进行了5次“读者调查问卷”，结果如下：

（1）计算表中各个频率；
（2）读者对该杂志满意的概率约是多少？
（3）从中你能说明频率与概率的关系吗？

设甲数为a，乙数为b，则甲、乙两数的平方和是

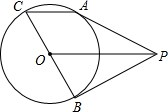如图所示，BC是⊙O的直径，P为⊙O外的一点，PA、PB为⊙O的切线，切点分别为A、B．试证明：AC∥OP．

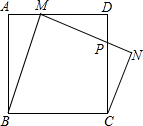如图，正方形ABCD中，M为边AD的一动点（不与点A、D重合），作等腰梯形BMNC，其中BM∥CN，BC=MN，MN与CD交于点P，若AB=1，AM=x，CP=y，则y关于x的函数关系式为y=

．

试题分类