题目内容
10. 如图直角坐标系中,直线l:y=kx+k经过A、B两点;点B(0,3);点P以每秒1个单位长度的从原点开始在y轴的正半轴向上匀速运动;设运动时间为t秒,直线y=t经过点P,且随P点的运动而运动.
如图直角坐标系中,直线l:y=kx+k经过A、B两点;点B(0,3);点P以每秒1个单位长度的从原点开始在y轴的正半轴向上匀速运动;设运动时间为t秒,直线y=t经过点P,且随P点的运动而运动.(1)求k的值和点A坐标;
(2)当t=1.5秒时,直线y=t与直线l交于点M,反比例函数y=$\frac{n}{x}$经过点M,求反比例函数的解析式;
(3)若直线y=t与直线l的交点不在第二象限,求t的取值范围;
(4)点C(3,0)关于直线l的对称点在直线y=t上,直接写出t的值.
分析 (1)把点B(0,3)代入y=kx+k,求出k的值,得出直线l的解析式,进而求出点A坐标;
(2)当t=1.5秒时,点P恰好是OB的中点,那么点M的纵坐标为1.5,将y=1.5代入直线l的解析式,求出M点坐标,再利用待定系数法即可求出反比例函数的解析式;
(3)直线y=t与直线l的交点不在第二象限时,交点在第一或第三象限,根据A、B纵坐标的值即可求出t的取值范围;
(4)设点C(3,0)关于直线l的对称点为C′,根据轴对称的性质得出直线l垂直平分线段CC′,设直线CC′的解析式为y=-$\frac{1}{3}$x+b,把C(3,0)代入,利用待定系数法求出直线CC′的解析式为y=-$\frac{1}{3}$x+1,设C′(x,-$\frac{1}{3}$x+1),根据AC′=AC,列出关于x的方程,解方程求出x的值,得到C′坐标,进而求解即可.
解答 解:(1)∵直线l:y=kx+k经过点B(0,3),
∴k=3,
∴直线l的解析式为y=3x+3,
令y=0,则3x+3=0,解得x=-1,
∴点A坐标为(-1,0); (2)∵当t=1.5秒时,OP=1.5,
(2)∵当t=1.5秒时,OP=1.5,
而B(0,3),
∴点P恰好是OB的中点;
又∵直线y=t与x轴平行,
∴点M的纵坐标为1.5;
∵点M又在直线l上,
∴3x+3=1.5,解得x=-0.5;
∴M(-0.5,1.5).
∵反比例函数y=$\frac{n}{x}$经过点M,
∴n=-0.5×1.5=-$\frac{3}{4}$,
∴反比例函数的解析式为y=-$\frac{3}{4x}$;
(3)∵A(-1,0),B(0,3),
∴根据图象,可知直线y=t与直线l的交点不在第二象限时,t的取值范围是t≤0或t≥3; (4)设点C(3,0)关于直线l的对称点为C′,
(4)设点C(3,0)关于直线l的对称点为C′,
则直线l垂直平分线段CC′,
∵直线l的解析式为y=3x+3,
∴可设直线CC′的解析式为y=-$\frac{1}{3}$x+b,
把C(3,0)代入,得-1+b=0,
解得b=1,
∴直线CC′的解析式为y=-$\frac{1}{3}$x+1,
设C′(x,-$\frac{1}{3}$x+1),
∵AC′=AC,A(-1,0),C(3,0),
∴(x+1)2+(-$\frac{1}{3}$x+1)2=42,
解得x1=-$\frac{21}{5}$,x2=3(舍去),
∴x=-$\frac{21}{5}$,
∴C′(-$\frac{21}{5}$,$\frac{12}{5}$),
∵点C′在直线y=t上,
∴t的值为$\frac{12}{5}$.
点评 本题考查了反比例函数与一次函数的交点问题,利用待定系数法求一次函数、反比例函数的解析式,轴对称的性质,函数图象上点的坐标特征等知识,有一定难度.利用数形结合是解题的关键.

| A. | (2,3) | B. | (-2,3) | C. | (2,-3) | D. | (2,-3)或(-2,-3) |
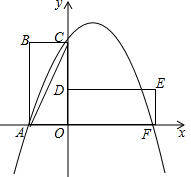 如图,在平面直角坐标系中,矩形OABC的边OA在x轴的负半轴上,边OC在y轴的正半轴上,且OA=1,tan∠ACB=2,将矩形OABC绕点O按顺时针方向旋转90°后得到矩形ODEF.点A的对应点为点D,点B的对应点为点E,点C的对应点为点F,抛物线y=ax2+bx+2的图象过点A,C,F.
如图,在平面直角坐标系中,矩形OABC的边OA在x轴的负半轴上,边OC在y轴的正半轴上,且OA=1,tan∠ACB=2,将矩形OABC绕点O按顺时针方向旋转90°后得到矩形ODEF.点A的对应点为点D,点B的对应点为点E,点C的对应点为点F,抛物线y=ax2+bx+2的图象过点A,C,F. 如图,直线a∥b,∠1=60°,∠2=50°,则∠3=70°.
如图,直线a∥b,∠1=60°,∠2=50°,则∠3=70°.