题目内容
8.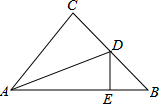 如图,三角形ABC中,∠C=90°,∠BAC的平分线交BC于D,DE⊥AB于E,已知CD=3,BD=5,求三角形ABC的周长.
如图,三角形ABC中,∠C=90°,∠BAC的平分线交BC于D,DE⊥AB于E,已知CD=3,BD=5,求三角形ABC的周长.
分析 根据角平分线的性质得到DE=CD=3,根据勾股定理求出BE的长,再根据勾股定理列出方程,解方程得到答案.
解答 解:∵AD是∠BAC的平分线,∠C=90°,DE⊥AB,
∴DE=CD=3,AC=AE,
∵DE⊥AB,DE=3,BD=5,
根据勾股定理得,BE=4,
∴AC2+82=(AE+4)2,
解得AE=6,
则AC=6,
∴三角形ABC的周长=AC+AB+BC=24.
点评 本题考查的是角平分线的性质和勾股定理的应用,掌握角的平分线上的点到角的两边的距离相等是解题的关键.

练习册系列答案
相关题目
20.一个口袋中装有12个乒乓球,其中3个球涂成黄色,5个球涂成绿色,4个球涂成红色.从中任意摸出一个乒乓球,这个球是红色的概率为( )
| A. | $\frac{1}{2}$ | B. | $\frac{1}{3}$ | C. | $\frac{1}{4}$ | D. | $\frac{1}{6}$ |
17.甲、乙、丙、丁四名参赛选手在预赛中所得的平均成绩$\overline{x}$及其方差S2如下表所示:如果选拔其中一人参加决赛,综合考虑,应是( )
| 甲 | 乙 | 丙 | 丁 | |
| $\overline{x}$ | 90 | 92 | 92 | 90 |
| S2 | 4.5 | 5 | 4.5 | 6.3 |
| A. | 甲 | B. | 乙 | C. | 丙 | D. | 丁 |
 如图,已知△ABC中,∠ABC的平分线与外角∠ACD的平分线相交于点I,∠A与∠BIC之间有怎样的数量关系?请说明理由.
如图,已知△ABC中,∠ABC的平分线与外角∠ACD的平分线相交于点I,∠A与∠BIC之间有怎样的数量关系?请说明理由.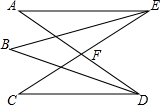 如图,EC与AD相交于F,EB、DB平分∠AEC、∠ADC交于点B.
如图,EC与AD相交于F,EB、DB平分∠AEC、∠ADC交于点B.